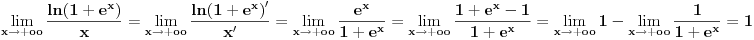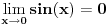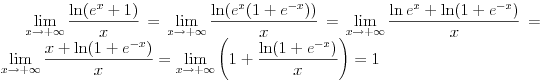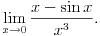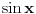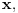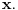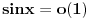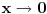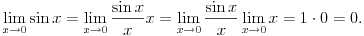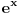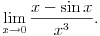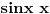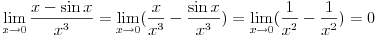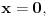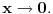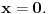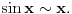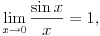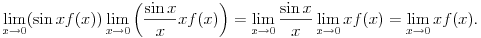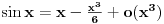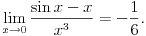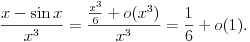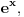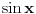
se može zameniti sa

samo kada je
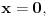
i nikad više! Ne može čak ni u graničnom procesu kada
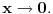
U Matematici se neštoz zamenjuje sa nečim drugim samo kada su te stvari jednake.
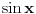
i

su jednaki samo kada je
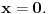
Međutim, kada
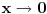
važi asimptotska relacija
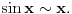
Ona je ništa drugo do kraći zapis formule
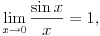
a to je matematička teorema, koja se stoga može koristiti uvek. U sledećem primeru je

bilo koja funkcija koja je definisana barem u nekoj šupljoj okolini nule.
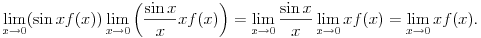
Naravno, neki međukoraci se mogu izostaviti ako podrazumevaju, pri čemu se to može raditisamo ako se na neki zna šta će se zaista dobiti. Što se tiče limesa za koji si pitao, on se može izračunati trostrukom primenom Lopitalovog pravila, kao i korišćenjem asimptotske relacije
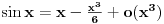
kada
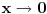
koja sledi iz Maklorenovog razvoja sinusa sa ostatkom u Peanovom obliku. Ona ne predstavlja ništa drugo do kraći zapis limesa
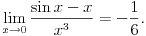
No, vratimo se na naš limes. On je očigledno isto što i prethodna relacija sa promenjenim znakom, ali ćemo ga raditi direktnom upotrebom Landauovih simbola. Naravno, sve se odnosi na granični proces kada
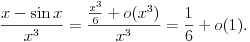
Što se tiče izvlačenja
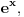
kada imak[ nekoliko sabiraka od kojih barem jedan po apsolutnoj vrednosti, onda izvlačiš napolje onaj koji najbrže teži beskonačnosti. Ako svi sabirci teže nuli, onda izvlačiš onaj koji najsporije teži nuli. U svakom slučaju, izvlačiš onaj sabirak u odnosu na koga su ostali "sitni".
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
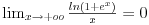
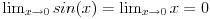
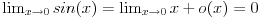




 Pomoc oko jednog limesa
Pomoc oko jednog limesa