• Naslovna
• FAQ
• Pravilnik
• O ES-u
• Tim
• Korisnici
• Statistike

 

• elitesecurity ::
• elitemadzone ::
• EMAIL ::
• RSS ::
• ES Mobile

  Niste ulogovani?  Username :   Password:   

• Registracija
• Zaboravili ste password?
• Flashback ▲▼
• Login problem?

 

Pretraga:

 

Srodne teme 20.10.2002. Trazenje minimuma 12.05.2004. Jednakokraki trapez sa razlicitim uglovima na vec.. 01.02.2005. Zadatak iz geometrije sa septembarskog ispitnog r.. 21.08.2007. pomozite pocetniku 17.12.2005. Teziste trougla!!! 23.03.2006. if-else pocetnicki problem 11.04.2007. Izracunati stranice jednakokrakog trougla 11.09.2007. Zadatak iz geometrije 02.11.2007. [Zadatak] Naci hipotenuzu trougla 05.07.2008. sumnjiv zadatak. Navigacija Brisanje liste Aktuelne teme u ovom forumu: Logaritamska nejednakost Raspoređivanje slova Košarkaši lep zadatak Zanimljiv zadatak o uglovima trougla Stado Boga Sunca ... 2000 godina star .. Bertranov paradoks ili nije paradoks? Polukružnica i poluprečnik Školski trougao 3, 4, 5 Zadaci za upis u matematičku gimnazij.. Presek dve kocke Upisana kružnica u trouglu Projekcija tela na ravan trokut za vi osnovne Geometrija-trokut Trokut sa 2 poznate stranice Izaberite forum: Linux Linux aplikacije Linux desktop okruženja Linux hardware Windows desktop Windows aplikacije Zaštita Office Windows drajveri Office :: Word Office :: Excel Macintosh Mac hardware Mac software Iphone Enterprise Networking SOHO Networking Wireless Windows mreže Linux mreže Wireless :: WiMax Wireless :: Mikrotik Wireless :: Wireless oprema Linux/UNIX serveri i servisi Unix BSD Skript jezici Security Virtualizacija Cloud Computing Services Security :: Kriptografija i enkripcija .NET 3D programiranje Art of Programming Asembler C/C++ programiranje Kernel i OS programiranje Pascal / Delphi / Kylix Java Embedded sistemi Perl PHP Python Visual Basic 6 Veštačka inteligencija Security Coding XML GameDev - Razvoj Igara Ostali programski jezici PHP :: PHP za početnike PHP :: Smarty template engine .NET :: .NET Desktop razvoj .NET :: ASP.NET .NET :: WPF Programiranje C/C++ programiranje :: C/C++ za početnike Baze podataka MySQL Oracle Access MS SQL Firebird/Interbase PostgreSQL Fiksna telefonija VoIP Udruženje korisnika teleko.. GSM - telefoni GSM - upotreba GSM - servisiranje Mreže i novosti Smartphone Mreže i novosti :: Mobilni internet Mreže i novosti :: Telenor - korisnički servis Mreže i novosti :: VIP - korisnički servis Mreže i novosti :: MTS - korisnički servis Smartphone :: Symbian OS Smartphone :: Windows Mobile Smartphone :: Android GSM - telefoni :: Nokia PDA Uređaji GPS Portable Players Anonimnost i privatnost ISP Browseri E-mail Instant Messaging FTP Google Hosting ISP :: Wireless mreže i ISP ISP :: ADSL E-mail :: Anti-spam Instant Messaging :: IRC Hosting :: Domeni Google :: Gmail E-Marketing Web aplikacije Web dizajn i CSS Web dizajn softver Web razvoj Pretraživači i SEO Flash Javascript i AJAX Web dizajn i CSS :: Kritike Grafički dizajn Izdavaštvo 3D modelovanje Rasterska grafika Vektorska grafika 3D modelovanje :: CAD/CAM Matične ploče, procesori .. Video karte i monitori Storage Ostali hardver Overclocking & Modding PC Konfiguracije Laptopovi Vodič za kupovinu - PC har.. Tablet PC Muzička produkcija Audio kompresija Audio softver Video produkcija Video kompresija Video softver Multimedijalni uređaji Digitalni fotoaparati Digitalne kamere Home Theater Digitalni fotoaparati :: Fotografija Digitalni fotoaparati :: Vodič za kupovinu - Digita.. Elektronika Elektrotehnika Elektronika :: TV uređaji Elektronika :: Radio elektronika i tehnika Elektronika :: Mikrokontroleri Elektronika :: Audio-elektronika Auto-elektronika :: Tuning Vodič za učenje Vodič za posao Vodič za emigraciju Fizika Matematika Nauka Sertifikati Informatika Vodič za učenje :: Seminarski radovi Vodič za učenje :: Obrazovne institucije Vodič za emigraciju :: Život u USA Vodič za emigraciju :: Život u Norveškoj Vodič za emigraciju :: Život u Nemačkoj E-Poslovanje E-Kupovina IT pravo i politika razvoja IT događaji IT berza poslova IS i ERP Ekonomija Berza Cryptocoins IT berza poslova :: Arhiva IT berze poslova IT pravo i politika razvoja :: Registar Nacionalnog ID E-Poslovanje :: E-Transakcije E-Poslovanje :: Forex E-Kupovina :: Platne kartice Digitalna Televizija Advocacy Ankete Predlozi i pitanja Vesti Čekaonica Vesti :: ES leto manifestacija MadZone TechZone Poljoprivreda AutoZone MotoZone Svakodnevnica Video igre MadZone :: Zanimljivi linkovi MadZone :: Kultura TechZone :: Ergonomija TechZone :: Grejanje TechZone :: Klimatizacija TechZone :: Bela tehnika AutoZone :: Fiat Panda club Lista poslednjih: 16, 32, 64, 128 poruka.

jans Član broj: 218504 Poruke: 34 *.dynamic.a1.rs. +2 Profil Zanimljiv zadatak o uglovima trougla 23.12.2024. u 21:15 - pre 32 dana i 22h Nedavno sam "naišao" na ovaj zadatak. Nije težak, zanimljiv je i poučan, pa ga postavljam na forum ( a i da razbijem monotoniju ). Pa ko voli ( geometriju ) nek izvoli. Na stranici BC trougla ABC data je tačka D takva da je CD=2DB i ugao U(B,A,D)=15o. Naći uglove trougla ako je ugao kod temena B veličine 45o. Napomonjem da se ti uglovi, ako se trougao nacrta, lako mogu odrediti merenjem. Međutim, takva " rešenja " nisu regularna. Prikačeni fajlovi Sl. 1.png - 16.04k Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8670 *.dynamic.isp.telekom.rs. +2795 Profil Re: Zanimljiv zadatak o uglovima trougla 24.12.2024. u 13:31 - pre 32 dana i 6h Evo šta je šablonsko rešenje: Nacrta se sve korišćenjem lenjira, šestara i uglomera i izmere uglovi. Tako znamo koji su iskazi tačni i ostajemo samo da ih dokažemo. Traženi ugao je 75 stepeni. Dvostruka vrednost je 150 stepeni. Tangens traženog ugla je pozitivan, a tangens dvostrukog ugla je . Ako to dokažemo, onda iz pozitivnosti traženog ugla zaključujemo da je ugao oštar, a iz tangensa dvostrukog ugla da je ugao oblika zaneko celobrojno , pri čemu je jedino rešenje . Dakle, treba izračunati tangens traženog ugla i tangens dvostrukog ugla. Najpre se sve postavi u koordinatni sistem (može se odabrati da je duž BD jedinična) i odrede koordinate presečne tačke pravih AB i AD. Onda se lako odredi i tangens traženog ugla, koji se najpre racionališe, a onda izračuna tangens dvostrukog ugla po formuli za tangens dvostrukog ugla. Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

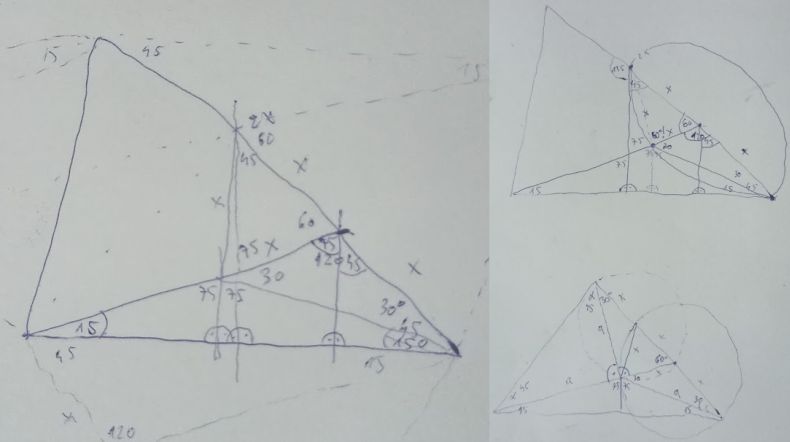
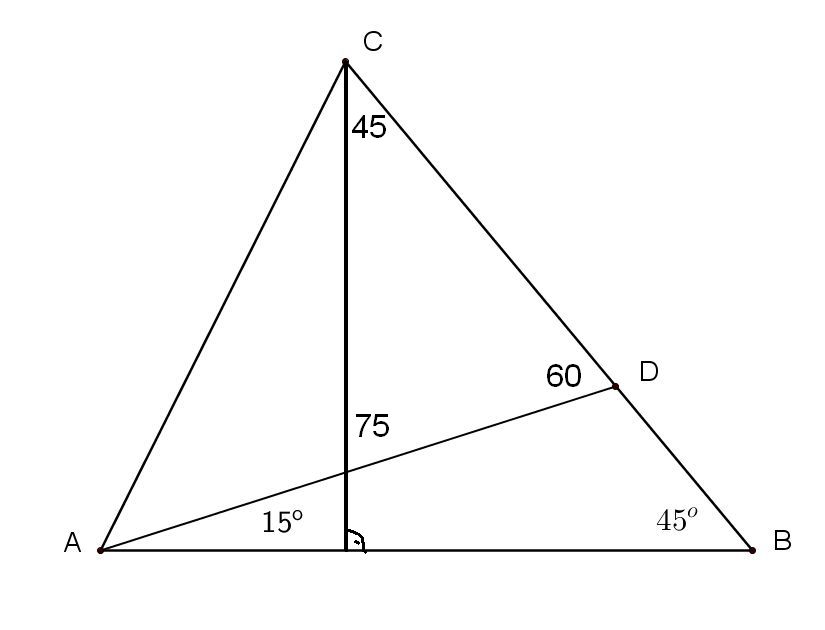
MajorFatal Milija Jakic opravljam oluke, 1337LAB Bg Član broj: 36595 Poruke: 1488 87.116.160.* +577 Profil Re: Zanimljiv zadatak o uglovima trougla 25.12.2024. u 17:10 - pre 31 dana i 2h U trouglu ABD treći ugao je 120 stepeni, njemu spoljni ugao ADC je 60 stepeni. Po uslovu zadatka CD = 2DB, ako DB obeležimo kao X, CD = 2X, ali umesto 2X, na sredini duži CD odredim tačku i nazovem je E, pa umesto CD = 2X pišem CE = X i ED = X ... Iz ugla kod B da se konstruisati duž ili poluprava pod uglom od 15 stepeni u odnosu na AB, ta poluprava presećiće AD u novoj tački F. Ujedno poluprava je ugao od 45 stepeni kod temena B podelila na uglove od 15 i 30 stepeni. Trougao ABF je jednakokraki, sa dva ugla od po 15 stepeni, preostali ugao kod F je 150 stepeni, njemu spoljašnji ugao BFD je 30 stepeni. Trougao BFD je jednakokraki, jer ima dva ugla po 30 stepeni, pa je i dužina FD takođe jednaka X kao i BD ... Ako spojim tačke E i F, dobiće se jednakokraki trougao koji ima dve stranice dužine X, to su stranice ED i FD, međutim ugao između njih je 60 stepeni, sledi da preostala dva ugla u zbiru daju 120 stepeni, a pošto su međusobno jednaki da su oba po 60 stepeni, to jest da je trougao FED jednakostranični ... 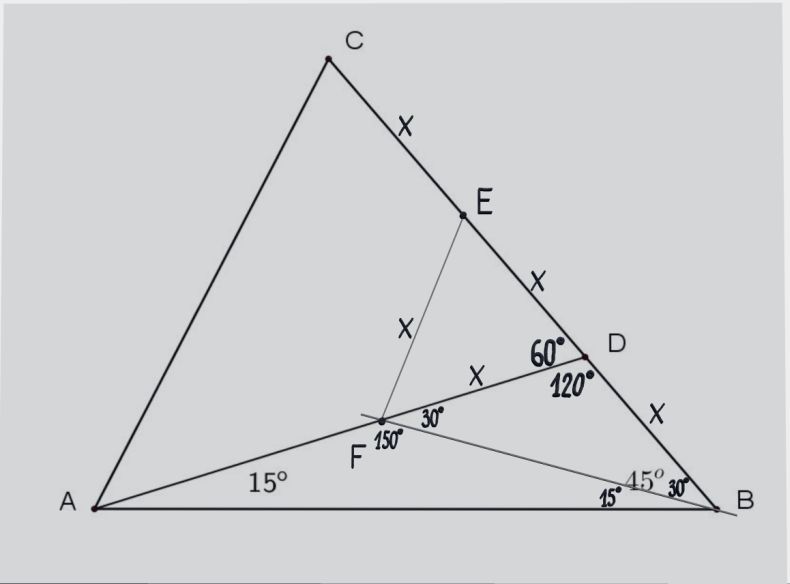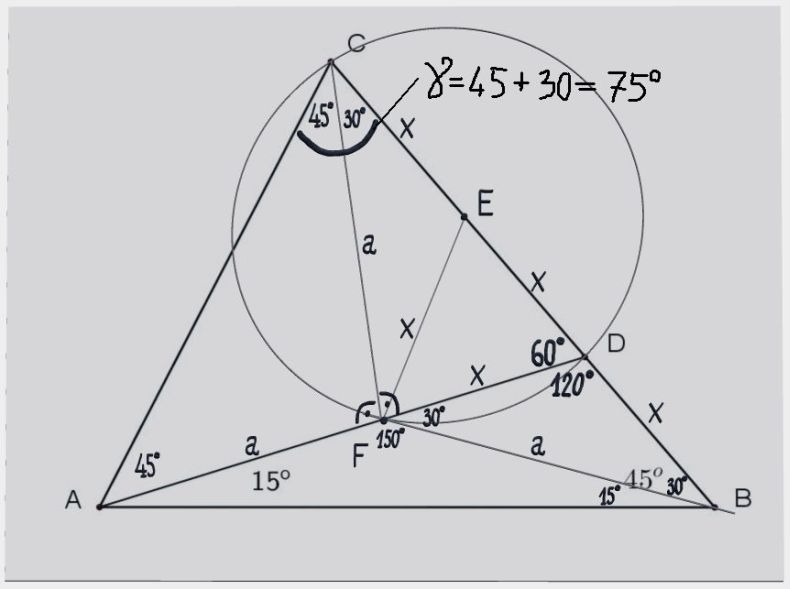S obzirom da su tačke C, D i F podjednako, za udaljenost X, udaljene od tačke E moguće je konstruisati kružnicu sa centrom u E, koja prolazi kroz sve tri tačke C, D i F. Duž CD je prečnik te kružnice, a ako spojimo tačke C i F, trougao DFC je konstruisan iznad prečnika kružnice i trećim temenom F leži na kružnici. Svaki takav trougao konstruisan iznad prečnika sa trećim temenom na kružnici je pravougli, sa pravim uglom kod temena koje leži na kružnici (mimo prečnika) u ovom slučaju kod temena F, ugao DFC je prav, i iznosi 90 stepeni. Njemu spoljni ugao AFC je takođe prav i iznosi 90 stepeni. S obzirom da su u trouglu DFC uglovi 60 i 90 stepeni, sledi da je treći ugao, kod trećeg temana C jednak 30 stepeni, tj ugao FCD = 30 stepeni. Trougao ABF je jednakokraki, sa dva ugla po 15 stepeni, ako dužinu BF označimo kao a, drugi krak AF će takođe biti dužine a. I trougao BFC je takođe jednakokraki, sa dva ugla od po 30 stepeni, pošto smo dužinu BF obeležili kao a, i dužina CF će isto iznositi a. Trougao AFC je isto jednakokraki, sa dve katete koje su dužine a, između je prav ugao, sledi da su preostala dva ugla jednaka i da iznose po 45 stepeni, tj uglovi FAC i FCA = 45 stepeni. Traženi ugao ACB jednak je zbiru uglova ACF i FCD to jest jednak 45 + 30 = 75 stepeni. Preostali ugao u trouglu BAC jednak je 45 + 15 = 60 stepeni. Nemoj da pricas? Prikačeni fajlovi uglovi2b.jpg - 20.87k uglovi4b.jpg - 31.3k Odgovor na temu

feveh Član broj: 350462 Poruke: 4 +1 Profil Re: Zanimljiv zadatak o uglovima trougla 25.12.2024. u 17:20 - pre 31 dana i 2h Imamo ugao BDA 120 stepeni ugao ADC 60 stepeni ugao (alfa1) DAB 15 steni ugao (beta) ABC 45 sstepeni i nepoznat ugao (alfa2) DAC. Ako je alfa unutrašnji ugao tačke A trougla ABC i gama unutrašnji ugao temena C tog trougla tada je: alfa = alfa1 + alfa2 alaf1 = 15 alfa2 + gama = 120 alfa = 135 - gama, 0 < gama < 135. Tek toliko da osetimo problem. A sad račun uz uobičajene oznake: a = 3 DC = 2 sin(120)/c = sin(15)/1 c=sin(120)/sin(15) sin(45)/AD = sin(15)/1 AD = sin(45)/sin(15) b^2 = AD*AD + DC*DC - 2 * AD * DC * cosin(60); Izračunao sam b^2 i c, a je zadato. Imam trougao ABC, pa je cos(alfa) = (b^2 + c^2 - a^2) / (2*b*c) = 0.5 odakle alfa=60, gama=75. Ja sam bio dovoljno lud da sve to računam a ko je pametan nek proveri. Odgovor na temu

jans Član broj: 218504 Poruke: 34 *.dynamic.a1.rs. +2 Profil Re: Zanimljiv zadatak o uglovima trougla 25.12.2024. u 20:25 - pre 30 dana i 23h U prethodna tri posta imamo tri različita rešenja zadatka. Nedeljko je rešio zadatak, i on sam kaže, „šablonski“. Postupak koji navodi feveh, iako jednostavniji od prethodnog, takođe je šablonski. Razlog za postavljanje ovog zadatka na forum je treći način rešavanja, bez analitičke geometrije i trigonometrije. Taj način je kraći od prethodnih, iziskuje samo osnovno poznavanje geometrije, a svodi se na primenu podudarnosti truouglova ( to smo učili u VI osnovne ). „Najbliže“ tom rešenju je rešenje koje navodi MajorFatal, samo što ga je on malo zakomplikovao. Rešenje može biti jednostavnije i kraće. Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8670 *.dynamic.isp.telekom.rs. +2795 Profil Re: Zanimljiv zadatak o uglovima trougla 25.12.2024. u 22:32 - pre 30 dana i 21h Razlog mog načina pisanja (zanemarujući očigledne jezičke greške) je opštost. Kako izaći iz okvira ovog jednog zadatka i rešavati mnoge slične zadatke? Štosovima koji su primenljivi samo na jedan zadatak se pribegava kada nema drugog rešenja, a radi se o nekoj važnoj činjenici. Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

MajorFatal Milija Jakic opravljam oluke, 1337LAB Bg Član broj: 36595 Poruke: 1488 87.116.160.* +577 Profil Re: Zanimljiv zadatak o uglovima trougla 26.12.2024. u 13:09 - pre 30 dana i 6h Pa i ja sam rešavao tako da bude univerzalno rešenje, da ne trebaju tangensi, sinusi .. :) Ču ja zakomplikovao, ja još i skratio, ispustio sam da napišem da tek kad se pokaže da je FED jednakostraničan, tek tad može da se napiše da je FE = X .. A vi gospodine jans, zašto ste koristili dva različita fonta za ispisivanje vrednosti uglova, hteli ste da nas zbunite da ne rešimo zadatak? Nemoj da pricas? Prikačeni fajlovi font.jpg - 4.18k Odgovor na temu

feveh Član broj: 350462 Poruke: 4 +1 Profil Re: Zanimljiv zadatak o uglovima trougla 26.12.2024. u 15:15 - pre 30 dana i 4h Baš me zanima "cena" dokaza da je FE == X :) @jans je dobar matematičar i pretpostavio sam da ima na umu primenu stavova podudarnosti. Ali sam od konstruktivnog dokaza za VI razred osnovne odustao kad sam video da na prave odredjene sa AB, AC i AD ne mogu da primenim teoremu o nesusednim uglovima. Odnosno konstruktivni dokaz se toliko komplikuje da gubi smisao a ta konstrukcija ima ograničenu primenu. Zato sam se okrenuo trigonometriji a prednost takvog prilaza je što dobijam numeričku vrednost. Rešenje metodama anlitičke geometrije ima svoju neposrednu primenu u na primer računarskim animacijama ili u artiljeriji. Ako tačku A postavimo u centar koordinatnog sistema onda je lako odrediti nagib prave BC a time i koordinate tačke C. Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8670 *.dynamic.isp.telekom.rs. +2795 Profil Re: Zanimljiv zadatak o uglovima trougla 27.12.2024. u 04:13 - pre 29 dana i 15h Prema ideji i oznakama člana MajorFatal: Neka je E središte duži CD. Tada je CE=ED=DB. Ovu dužinu označimo sa x. Ugao ADB je 120 stepeni (jer je zbir uglova u trouglu ADB jednak 180 stepeni), pa je ugao CDA 60 stepeni. Neka je F tačka na duži AD tako da ugao DBF bude 30 stepeni i samim tim podudaran uglu DFB. Važi DF=DB=x. Pošto je ugao CDA 60 stepeni, važi EF=x. Tačke C, D i F leže na krugu sa centrom E, pa je ugao CFD je prav kao periferijski nad prečnikom CD, pa je ugao EFC jednak 30 stepeni. Iz FE=EC zaključujemo da je ugao ECF podudaran uglu EFC koji je 30 stepeni, pa je BF=BC. Iz AF=BF=BC sledi da su uglovi FAC i FCA podudarni, pa pošto je ugao AFC prav, ugao ACF je 45 stepeni, pa je ugao CAD jednak 75 stepeni. Ne znam da li sada neko ima nedoumica oko njegovog rešenja. Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

MajorFatal Milija Jakic opravljam oluke, 1337LAB Bg Član broj: 36595 Poruke: 1488 87.116.160.* +577 Profil Re: Zanimljiv zadatak o uglovima trougla 27.12.2024. u 19:56 - pre 28 dana i 23h Eh, hvala Nedeljko, ja stvarno "preko brda i dolina" kako je govorila nastavnica matematike svojevremeno, kad ispišemo rešenje koje je duže nego što bi trebalo. Možda je mogla samo da se spusti normala iz tačke C na AD, isto bi se dobila tačka F, takođe simetrala duži BC dala bi F i na dalje sve isto. Primetio sam i da se trouglovi EFB i DFC slični, pa se negde tu možda krije neko kraće rešenje za koje pita jans ... Nemoj da pricas? Odgovor na temu

feveh Član broj: 350462 Poruke: 4 +1 Profil Re: Zanimljiv zadatak o uglovima trougla 27.12.2024. u 23:08 - pre 28 dana i 20h To "cena" nije osporavanje tačnosti ni metoda ni dokaza nego se odnosi na vreme, ljudske i računarske resurse utrošene na pronalaženje rešenja. Meni izgleda da je za pronalaženje tog rešenja korišćena neka aplikacija za inženjerske konstrukcije. To nije isto kao rad "peške". Odgovor na temu

miki069 Član broj: 161528 Poruke: 2012 *.mbb.yettel.rs. +382 Profil Re: Zanimljiv zadatak o uglovima trougla 28.12.2024. u 11:26 - pre 28 dana i 8h Pošovani kolega Jans je trebao da definiše za koji nivo je zadatak. Ako je za 6,7,8 razred osnovne škole, onda jedino korektno rešenje je ono koje je dao Major. Odgovor na temu

MajorFatal Milija Jakic opravljam oluke, 1337LAB Bg Član broj: 36595 Poruke: 1488 87.116.160.* +577 Profil Re: Zanimljiv zadatak o uglovima trougla 28.12.2024. u 12:16 - pre 28 dana i 7h Citat: feveh: To "cena" nije osporavanje tačnosti ni metoda ni dokaza nego se odnosi na vreme, ljudske i računarske resurse utrošene na pronalaženje rešenja. Meni izgleda da je za pronalaženje tog rešenja korišćena neka aplikacija za inženjerske konstrukcije. To nije isto kao rad "peške". Naravno da je korišćena inžinjerska aplikacija Kliker.com ChatGpt 6.01, ali su još zanimljiviji hardveri na kojima je tarana, tkz papir i olovka .. sa mnogo predomišljanja i odustajanja. Nego sad kad si me naterao da ponovo pogledam slike, jedva sam se otarasio ove druge kružnice koju sam crtao u centru sa D, te video da mi ne treba dva ugla od po 75, međutim u međuvremenu se ispostavilo da je 75 rešenje, tako da ako se spusti normala iz C na AB odmah se dobija trougao koji je sličan trouglu ABC, jedino što ne znam kako bih dokazao da su slični :) Možda na to mnogo kraće rešenje aludira jans .. Nemoj da pricas? Prikačeni fajlovi soft3.jpg - 22.36k uglovi5.jpg - 20.45k Odgovor na temu

miki069 Član broj: 161528 Poruke: 2012 *.mbb.yettel.rs. +382 Profil Re: Zanimljiv zadatak o uglovima trougla 29.12.2024. u 17:20 - pre 27 dana i 2h Nisam stigao ni da pokušam da rešim zadatak. Molio bih pošovanog kolegu Jansa, da u 20024-toj godini ne objavljuje to kraće rešenje. Da probaju i ostali. Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8670 *.dynamic.isp.telekom.rs. +2795 Profil Re: Zanimljiv zadatak o uglovima trougla 31.12.2024. u 16:20 - pre 25 dana i 3h Malo drigačije rešenje. Prvo se odrede laki uglovi. Tačka E se izabere kao simetrala duži CD. Duži CE, ED i DB. Obzirom da je ugao ADC jednak 60 stepeni, tačka F se izabere tako da trougao DEF bude jednakostranični. Trougao BDF je jednakokraki pa uglovi FBD o BFD imaju po 30 stepeni. Trougao BCF je simetričan u odnosu na simetralu stranice BC, pa je jednakokraki, pa ugao ECF ima 30 stepeni. Trougao CFE je jednakokraki, pa ugao CFE ima 30 nstepeni, pa je ugao CFA prav. SVaka od duži AF i CF je podudarna duži BF, pa je trougao AFC jednakokraki, pa uglovi CAF i AFC imaju po 45 stepeni. Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

miki069 Član broj: 161528 Poruke: 2012 *.mbb.yettel.rs. +382 Profil Re: Zanimljiv zadatak o uglovima trougla 31.12.2024. u 18:57 - pre 25 dana Trebalo je samo da se spusti visina iz temena C na duž AD. To je tačka F. Da bi se iskoristila osobina da se u pravouglom trouglu naspram ugla od 30 stepeni nalazi kateta duplo manja od hipotenuze. Račun je objasnio Nedeljko. [Ovu poruku je menjao miki069 dana 31.12.2024. u 20:08 GMT+1] Odgovor na temu

miki069 Član broj: 161528 Poruke: 2012 *.mbb.yettel.rs. +382 Profil Re: Zanimljiv zadatak o uglovima trougla 31.12.2024. u 19:54 - pre 25 dana Bez ove Nedeljkove ideje, račun preko: jednom kosinusna i 3 puta sinusna teorema nije toliko mnogo smoran. Problem je bio da se prepozna potpun kvadrat (žuta boja). Prikačeni fajlovi Sinus-Kosinus.pdf - 100.86k Odgovor na temu

miki069 Član broj: 161528 Poruke: 2012 *.mbb.yettel.rs. +382 Profil Re: Zanimljiv zadatak o uglovima trougla 01.01.2025. u 08:41 - pre 24 dana i 11h Zadatak liči na: https://www.elitesecurity.org/t480726-0#3515544 Ne po tekstu, nego po tome koliko je teže rešiti ga upotrebom trigonometrije. Odgovor na temu

jans Član broj: 218504 Poruke: 34 *.dynamic.a1.rs. +2 Profil Re: Zanimljiv zadatak o uglovima trougla 01.01.2025. u 12:13 - pre 24 dana i 7h Postupak rešavanja je najkraći, to je u jednom od prethodnih postova konstatovao i miki069, ako koristimo samo tačku F. Tačka E je suvišna. A tačku F na duži AD možemo odrediti na tri načina: - tako da ugao ABF bude 15o; - tako da bude DF=DB; - kao podnožje normale iz temena C na duž AD. Bez obzira kako tačku F odredimo, postupci rešavanja se razlikuju samo u redosledu primene osobina trougla ( osobine uglova trougla, jednakokrakih trouglova i, posredno, podudarnost trouglova ). Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8670 *.dynamic.isp.telekom.rs. +2795 Profil Re: Zanimljiv zadatak o uglovima trougla 01.01.2025. u 20:30 - pre 23 dana i 23h Pokretač teme je u početnoj poruci tvrdio da je zadatak počan. Po čemu je poučan? Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu