Što se drugog načina tiče, neka je
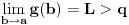 .
.Za ma koje
 postoji
postoji 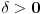 takvo da za svako
takvo da za svako 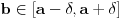 važi
važi 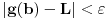 . Tada zbog
. Tada zbog 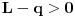 stavljajući
stavljajući 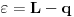 zaključujemo da postoji
zaključujemo da postoji  takvo da je
takvo da je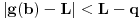 ,
,a samim tim i
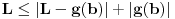 ,
,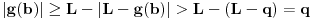 ,
,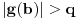 .
.Dakle, pošto je
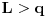 , a
, a 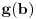 može biti po želji blisko
može biti po želji blisko  (na osnovu izbora
(na osnovu izbora  i definicije limesa), a ako je tako, onda je i
i definicije limesa), a ako je tako, onda je i 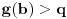 .
.Ovde je naravno
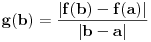 .
.Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.




 Re: Kontrakcija i primena Banahovog stava o fiksnoj tacki
Re: Kontrakcija i primena Banahovog stava o fiksnoj tacki


