Kod prvog zadatka je greška uzimati da koren broja može biti manji od nule - koren se uzima da je uvek pozitivan, a za rešenja npr.
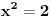
se uzima
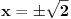
, ali sam koren pozitivnog broja je uvek pozitivan.
Za deljivost sa 6 broj ne mora biti deljiv sa 12, već samo sa 2 i 3 (12 je deljiv i sa 4, što nije potrebno za deljivost sa 6, recimo 18 nije deljivo sa 12, ali je deljivo sa 6, kao i npr. 30, 42, itd.).
Blessed are those who can laugh at themselves, for they shall never cease to be amused.