Neprazan, zatvoren skup bez izolovanih tačaka zove se savršen skup. Zatvorenje preseka savršenog i otvorenog skupa je ili prazan skup ili savršen skup.
Neka su

i

ma koje tačke savršenog skupa

i neka je
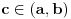
. Neka je
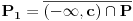
i
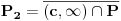
. Time je savršen skup podeljen na dva savršena podskupa koja imaju najviše jednu zaedničku tačku.
Obzirom da radimo sa kompaktima, možemo osigurati da nijedan od skupova
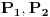
nema dijametar veći od polovine dijametra skupa

.
Na taj način se može definisati jedno beskonačno binarno drvo savršenih skupova čiji je koren dati kompakt, pri čemu je unija dece bilo kog čvora jednaka čvoru, deca istog čvora imaju najviše jednu zajedničku tačku i dete ima dijametar majmanje duplo manji od roditelja.
Neka je

bilo koji realan broj iz intervala

, ali koji nije oblika
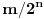
i neka je
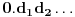
njegov binarni zapis. Odgovarajući binarni zapisi su tačno oni koji se ne završavaju nulama ili jedinicama. Uočimo granu formiranog drveta koja odgovara tom nizu cifara. Dakle, 0 - levo, 1 - desno. Presek skupova na toj grani je jednočlan skup i njegov element neka bude

.
Ovim smo formirali bijekciju između intervala

bez prebrojivo mnogo tačaka i kompakta

bez prebrojivo mnogo tačaka, čime možemo sa prvog od ta dva skupa da prenesemo meru (Lebegovu) na drugi. Uz dodatak da prebrojivi skupovi imaju meru nula i komplement datog kompakta ima meru nula dobijamo traženu meru.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.