Pretpostavimo da je
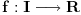
monotono neopadajuća funkcija čiji je domen zatvoren interval. Neka je
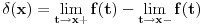
za
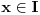
, pri čemu uzimamo da je
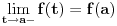
ako je
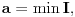
odnosno
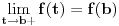
ako je
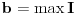
(ako takvi elementi uopšte postoje). Korišćenjem monotonije funkcije

jednostavno se dokazuje da ako je

i
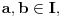
onda mora da važi
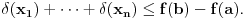
No, odatle sledi da je
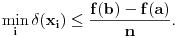
Pretpostavimo da su sve od tačaka

tačke prekida funkcije
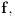
odnosno da je
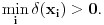
Tada je
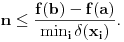
To upravo znači da za svako

na ma kom ograničenom intervalu postoji najviše konačno mnogo tačaka

takvih da je
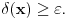
Pošto je svaki interval prebrojiva unija nekih ograničenih intervala, na ma kom intervalu će za svako

postojati nejviše prebrojivo mnogo tačaka

takvih da je
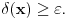
Neka je
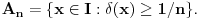
Prema prethodnom su svi od skupova
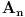
prebrojivi, a pošto je skup tačaka prekida funkcije

jednak uniji tih skupova, onda i on mora biti najviše prebrojiv.
[Ovu poruku je menjao Nedeljko dana 18.08.2005. u 11:17 GMT+1]
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.