pa mozda moze i ovako :)
Teorija: Proizvod tri sukcesivna (uzastopna) prirodna broja je uvijek djeljiv sa tri.
Prema gore navedenom, treba dokazati da se gorinji izraz ili njegov dio moze prikazati kao proizvod tri sukcesivna prirodna broja. Pretpostavljamo da je u uslovima zadatka
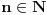
. Prema tome imamo:
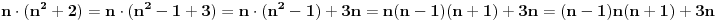
*
pošto izraz
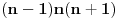
predstavlja proizvod tri sukcesivna prirodna broja, to je on djeljiv sa 3 pa stoga možemo pisati
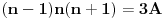
gdje je
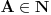
Na kraju se izraz * može napisati kao
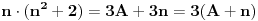
što je svakako djeljivo sa 3 jer je jedan faktor upravo broj 3. That's it without mathematical induction :)
MyCoNfa:
CPU: AMD Phenom II X4 965 3,4GHz BOX
Maticna:Asus M4A89GTD PRO
RAM: Corsair 4x2GB 1600MHz, 9-9-9-24
Grafa: Diamond ATI 5870 1GB
HDD:3xWD 320GB AAKS, stripe raid
DVD/RW:LG,SATA
SilverStone SST-ST50F 500W
CoolerMaster CM690
LG 24" 2453TQ-PF
Tastatura A4Tech X7 G800
Stakor: A4Tech X7-755FS