Citat:
CombatJazz:
Neka su c i d iracionalni brojevi, te (c+d)/2 iracionalan broj
Ovo nije tačno (kontraprimer:
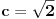
,
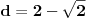
).
Citat:
petarm:
...i neprebrojivo beskonacni skupovi njihov kardinalni broj je
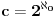
.
Pero, pazi bre šta pričaš.

Beskonačan skup je neprebrojiv (po definiciji) ako nije prebrojiv. O njegovom kardinalnom broju možemo reći samo da je veći od

, a takvih kardinalnih brojeva ima mnooogo (tj., ni slučajno
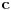
nije jedina mogućnost).
Ljubičice crvena, što si plava kô zelena trava.