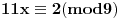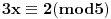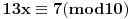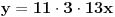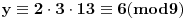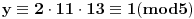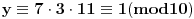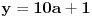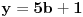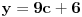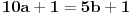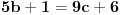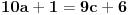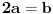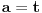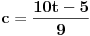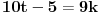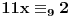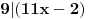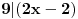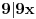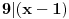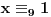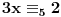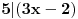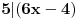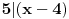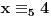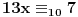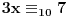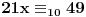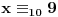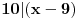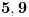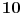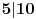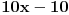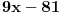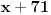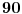[es] - rješavanje sistema kongruencija

melina7
student
BiH

Član broj: 272861
Poruke: 6
*.ze2.dlp192.bih.net.ba.

+5 Profil

^{01.01.2011. u 14:16 - pre 161 meseci}

Riješiti sistem kongruencija:
11x ≡ 2 (mod 9), 3x ≡ 2 (mod 5), 13x ≡ 7 (mod 10)

treba mi pomoc oko ovog sistema, vec par puta radim i ne mogu dobit dobro rjesenje. Buduci da moduli nisu relativno prosti u parovima onda se ovo dalje rastavi ? pa onda imamo sistem :
11x ≡ 2 (mod 9), 3x ≡ 2 (mod 5), kad rastavimo 13x ≡ 7 (mod 10) dobijamo:
x ≡ 1 (mod 2), 3x ≡ 2 (mod 5)

tj. konacni sistem
11x ≡ 2 (mod 9),
3x ≡ 2 (mod 5),
x ≡ 1 (mod 2).
--------------------
33x ≡ 6 (mod 27),
33x ≡ 22 (mod 55),
33x ≡ 33 (mod 66).
pa se uvodi smjena t=33 x

pa onda dobijamo sistem
t ≡ 6 (mod 27),
t ≡ 22 (mod 55),
t ≡ 33 (mod 66)

Da li dobro radim, ako ne u čemu griješim ?? hvala :)

Odgovor na temu

Fermion
ucenik

Član broj: 273771
Poruke: 237
*.mbb.telenor.rs.

+13 Profil

Re: rješavanje sistema kongruencija

^{01.01.2011. u 14:55 - pre 161 meseci}

Evo kako bih ja ovo rešio:
Imamo da je:

Svedimo sve ove kongruencije na broj

.
Tada je:

Pošto odredimo y onda možemo odrediti x iz

.

Koliko je y?

To se svodi na:

Pošto se odrede

može se odrediti i y, a zatim x.

Odgovor na temu

Fermion
ucenik

Član broj: 273771
Poruke: 237
*.mbb.telenor.rs.

+13 Profil

Re: rješavanje sistema kongruencija

^{01.01.2011. u 15:03 - pre 161 meseci}

Ovaj zadnji deo sa a,b,c ne može da se izvede direktno rešavanjem sistema, jer iz prve je

, što se dobija i oduzimanjem druge od treće jednačine, pa sistem ima beskonačno mnogo rešenja, ali se može naći rešenje ako se jedan od tih brojeva uzme kao parametar, a ostali izraze preko njega. Odatle dobijamo ako je

Broj u imeniocu se završava sa 5, i deljiv je sa 9 jer je c celobrojno.

Nađimo brojeve oblika

Pošto se leva straba završava sa 5 sledi da se k završava sa 5.

Treba da probamo brojrve 5, 15, 25, ...

Redom, 45 je premalo, 135 daje t=14, pa je y=161, štp je opet premalo (broj y je jednak 33*13 x pa je veći od 33*13).

Treba probati malo veće brojeve i bar jedan od njih bi trebao da zadovolji polazni sistem.

Ovo je dugačak postupak i njime se ne dokazuje da je rešenje jedinstveno, ali se skraćuje nasumično traženje na određenu klasu brojeva.

_{[Ovu poruku je menjao Fermion dana 01.01.2011. u 16:29 GMT+1]}

Odgovor na temu

Fermion
ucenik

Član broj: 273771
Poruke: 237
*.mbb.telenor.rs.

+13 Profil

Re: rješavanje sistema kongruencija

^{01.01.2011. u 16:56 - pre 161 meseci}

Evo još jedna ideja.

Znamo da je y=11*3*13*x = 429x.

Pošto ostatak pri deljenju y sa 10 iznosi 1 zadnja cifra je 1.

Ovim je jasno ispunjen i uslov da y daje ostatak 1 pri deljenju sa 5.

Prema tome x ne može biti paran broj.

S obzirom da broj y nije deljiv sa 9 sledi da x nije deljiv sa 3.

Zaključujemo da polazni sistem zadovoljava samo takvo x koje nije deljivo ni sa 3 ni sa 2, a da se y završava brojem 1. Poslednji uslov je ispunjen ako se x završava na 9, čime uslov nedeljeivosti sa 2 postaje ispunjen. Dakle treba nam x takvo da se završava sa 9, a nije deljivo sa 3. Prvi prirodan broj koji to zadovoljava je 19, međutim kod ovog broja ostatak deljenja y sa 9 nije 6. Zatim idemo na 29. Ovaj broj y ispunjava sve uslove kongruencija po y, ali ne ispunjava prvi uslov kopngruecija po x (po modulu 10). Zatim 39 ne zadovoljava kongruencije po modulu 9 sa y, kao ni broj 49. Broj 59 može po y, ne može po x. Nastavkom ovakve provere bi trebalo da se dođe do rešenja.

Naravno sve ovo su samo ideje, a ne kompletna rešenja.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8632
212.200.65.*

+2789 Profil

Re: rješavanje sistema kongruencija

^{01.01.2011. u 17:51 - pre 161 meseci}

Uslov