Da, Raselov paradoks. On, i slicni, su razlog da se malo ostrije postave temelji teorije skupova, verovatno najznacajnije u Matematici.
Mozda pomogne A7. aksioma regularnosti, u ZF teoriji (Zermelo-Fraenkel) :
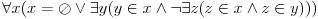
(izvor : "Hilbertovi problemi i logika" - Z. Mijajlovic, Z. Markovic i K. Dosen)
Tj. skup
x je ili prazan ili postoji element
y koga on sadrzi i on je takav da ne postoji
z sadrzan i u
x i u
y.
Ako skup
x sadrzi sebe, onda bi svi elementi skupa
x bili i elementi njegovog elementa, tj. opet skupa
x.
Secam se da je neko pricao i o "skupnim" osobinama i o onima koje to nisu. Pa je receno da osobina "biti element samoga sebe" nije skupna jer bi tvrdjenje da takav skup postoji bilo kontradikcija.