a) Skup

je konačan, pa ga možemo predstaviti kao
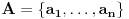
. Pošto je

surjektivna, važi
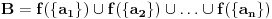
, pa pošto je
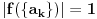
, sledi da je

(jednakost važi akko je f-ja i injektivna).
b) Pre svega, jasno je da za bilo koje skupove

i

važi
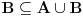
, tako da se tvoj zadatak svodi na dokaz
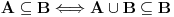
.
Neka je
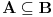
, onda ako je
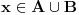
proizvoljano, imamo da je
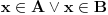
, pa na osnovu pretpostavke sledi da je
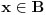
. Time je dokazano
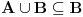
.
Neka je
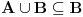
i neka
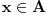
proizvoljno, onda, imamo da je
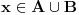
, a na osnovu pretpostavke i da je
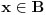
. Time je dokazano
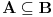
.
c) Nije prebrojiv, jer nije prebrojiv ni skup f-ja
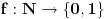
(ovo poslednje je lako dokazati).
Attempt all the problems. Those you can do, don't do. Do the ones you cannot.