Pre svega ostalog, dobio si dobar rezultat integracijom desne strane jednačine.
Tu imam samo jednu napomenu da je zdravije odabrati drugačiji indeks Lagerovog polinoma koji se nalazi u izrazu kojim množiš početnu jednačinu. Ako odabereš da taj indeks bude

umesto

(da ne bi došlo do zabune i grešaka u nastavku dokaza), onda množiš sa
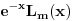
, gde je
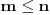
i kao rezultat posle integraljenja desne strane dobijaš:
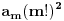
.
Sada je:
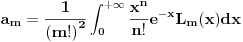
Posle uvrštavanja izraza za Lagerove polinome u obliku izvoda i niza parcijalnih integracija dobija se:
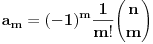
iz čega neposredno sledi dokaz.
"Verovatno da preko nje mnoge sile kontrolišu mnogo šta..." - GANDOR
"Kada bi ljudski mozak bio tako jednostavan da bismo mogli da ga shvatimo, onda bismo mi bili toliko glupi da ga ipak ne bismo mogli shvatiti."