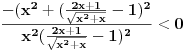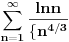Aha, znaci tako. Time dobijam da red konvergira. A tu aproksimaciju znaci mogu uvek da koristim kada imam oblik ln(n+c), n->beskonacno (c je konstanta)?
I samo jos jedno pitanje, da li sam dobro uradio ovaj zadatak:
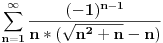
Dakle dobio sam da
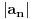
divergira, pa sam primenio Lajbnicov kriterijum da ispitam uslovnu konvergenciju.
Kako je limes
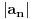
jednak 0, a
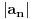
opadajuce (to sam zakljucio posto sam ga napisao kao funkciju f(x) i nasao prvi izvod f`(x)<0), red uslovno konvergira.