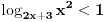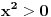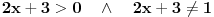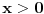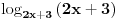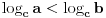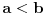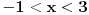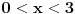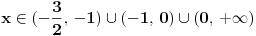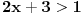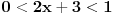Ljudi pomagajte MOLIM VAS.Ovo je vjerovatno ne tako tezak zadatak al meni ni naopako neide.Vi ste mi najveca sansa da dobijem rjesenje ovog zadatka.
Dakle, rijesiti logaritamsku nejednacinu: Log2x+3 x2 < 1 (ovo je log po bazi 2x+3 * x na kvadrat) ne znam kako ovo ubacit ovdje na forum u korektnom obliku,izvinjavam se...
HVALA na bilo kakvoj pomoci




 Logaritamska nejednacina
Logaritamska nejednacina