A i, joojj galet --
intuicija o mnogim stvarima ti je dobra ali, kao sto si sam rekao, nisi matematicki potkovan. To dovodi do mnogih konfuzija.
U matematici linija -- bilo prava, bilo kriva -- nema debljinu. Tacka. Zato ne mozes matematicki *tek tako* da pricas direktno o razlicitoj duzini unutrasnje i spoljasnje strane linije. Tacka.
Medjutim, tvoju intuiciju mozemo da spasemo putem sledeceg granicnog procesa:
Zamisli da imas beskonacno tanku (matematicku) liniju:
-----------------------
Onda iz svake tacke te linije mozes normalno da povuces jednu drugu linijcu.
|*|*|
|*|*|
----------
|*|*|
|*|*|
Onda po toj linijci sa obe strane originalne linije mozes da udaris recke jednako i jako malo (razdaljina
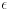
) udaljene od centra prvobitne linije:
x*x*x
|*|*|
----------
|*|*|
x*x*x
Ove dve serije recki -- isto tako beskonacno tanke -- prave dve dodatne linije "parallelne" i na rastojanju
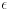
od prvobitne -- beskonacno tanke -- linije. Zajedno sa prvobitnom linijom, ove dve linije grade "traku" konacne debljine. Ova "traka" pak veoma lici na ono o cemu, koliko se meni cini, ti razmisljas.
Ako dve strane ove trake tj. dve reckaste linije imaju razlicitu duzinu, prvobitna linija je kriva. Ako imaju istu duzinu, prvobitna linija je prava.
Ukratko --
Matematicki je netacno da pricas o dve strane matematicke linije i o njihovim razlicitim duzinama (jer linija nema "dve strane")!
Medjutim, tvoja intuicija moze da se izvuce putem granicnog procesa kada pustis
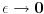
.
Dalje, po ovom kriterijumu pravu liniju moguce je kontinualno deformisati tako da postane kriva. Naravno, i pri najmanjoj konacnoj deformaciji ona ce postati kriva. Zato tebi izgleda da su "prava" i "kriva" linija dva sasvim drugacija pojma (ili nesto jeste 0 ili nije 0).
Medjutim, umesto da govorimo o kategoricnim pojmovima "pravo" i krivo, moguce je uvesti meru zakrivljenosti linije kao granicna vrednost
(duzina spoljasnje krive - duzina unutrasnje krive)/
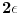
/(duzina centralne krive)
kada duzina centralne krive -> 0 i
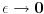
.
Ovo svodi na Cartanovu
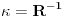
zakrivljenost krive gde je R tzv. "poluprecnik krivine". U slucaju kruga u ravnom prostoru, R odgovara poluprecniku tog kruga. Zbilja:
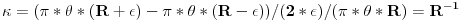
P.S.
Pazljiva analiza granicnih vrednost
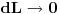
i
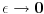
od izuzetne je vaznosti za logicku konsistentnost izlaganja.
Nazalost, granicni procesi poput ovog koji sam naveo mogu da budu veoma suptilni -- matematicarima je trebalo >150 godina (od Njutna do Weierstrass-a, Cantor-a i drugih) da ovakve procese koji se cesto koriste u fizici logicki potkuju. Zato pazljivo!