Srodne teme
Navigacija
Lista poslednjih: 16, 32, 64, 128 poruka.

Matematička indukcija

[es] :: Matematika :: Matematička indukcija

[ Pregleda: 11394 | Odgovora: 17 ] > FB > Twit

Postavi temu Odgovori

Autor
Pretraga teme: Traži
Markiranje Štampanje RSS

IdeaR
BiH

Član broj: 11048
Poruke: 126
*.as54.tz.bih.net.ba.



+2 Profil

icon Matematička indukcija05.06.2003. u 02:52 - pre 260 meseci
Ovo je zadatak broj 377. iz Zbirke zadataka iz više matematike 1, Uščumlić, Miličić, iz oblasti matematičke indukcije:

Dokazati da je [(2n)!]/[n!*(n+1)!] prirodan broj za svako n koje pripada N.

Zadatak ne znam riješiti, a bio bih zahvalan kada bi mi neko pokazao rješenje.

Pozdrav svima na forumu.
 
Odgovor na temu

goky2002

Član broj: 3848
Poruke: 191
*.ptt.yu



Profil

icon Re: Matematička indukcija05.06.2003. u 18:01 - pre 260 meseci
Lako je. Dokazes da vazi za 1.
Pretpostavis da vazi za n i onda uz pomoc te prertpostavke(koristeci je) dokazes da vazi za n+1.
 
Odgovor na temu

IdeaR
BiH

Član broj: 11048
Poruke: 126
*.as54.tz.bih.net.ba.



+2 Profil

icon Re: Matematička indukcija05.06.2003. u 21:15 - pre 260 meseci
Zahvljujem na podsjećanju na principe matematičke indukcije. Inače zadaci iz matematiče indukcije su vrlo lagani, i brzo se dokažu, ali ovaj gornji nikako ne uspijevam riješiti. Dakle, u gornjem zadatku ne mogu da pređem treći korak, ili ako hoćete, i drugi i treći jer su nerazdvojni. Opet molim ako neko zna riješti zadatak da to objavi, bio bih mu zahvalan.

Puno pozdrava svim matematičarima.
 
Odgovor na temu

random
Vladimir Vrzić
Beograd

Član broj: 85
Poruke: 3866
*.f.bg.ac.yu

Sajt: www.last.fm/user/vrza


+4 Profil

icon Re: Matematička indukcija06.06.2003. u 05:18 - pre 260 meseci
Da vidimo.



Za je

Ako pretpostavimo da je za za neko n f(n) ceo broj,







I sad treba dokazati da je ovaj razlomak celobrojan. A nije. Izgleda da sam negde pogrešio.
int rand(void);

Those who do not understand Unix are condemned to reinvent it, poorly.

Upali lampicu — koristi Jabber!
 
Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
*.ptt.yu



+64 Profil

icon Re: Matematička indukcija09.06.2003. u 00:14 - pre 259 meseci
Nije greška, nego je onaj koji treba da skrati sakriven. Ako budem imao vremena, potražiću ga.
 
Odgovor na temu

tOwk
Danilo Šegan
Zemun/Beograd

Član broj: 94
Poruke: 2743
*.beograd-3.tehnicom.net

ICQ: 9344053
Sajt: alas.matf.bg.ac.yu/~mm011..


+2 Profil

icon Re: Matematička indukcija09.06.2003. u 00:21 - pre 259 meseci
Pa treba još proveriti da je , možda može i to matematičkom indukcijom.
Možda se moje mišljenje promenilo, ali ne i činjenica da sam u pravu.
 
Odgovor na temu

IdeaR
BiH

Član broj: 11048
Poruke: 126
*.as54.tz-old.bih.net.ba



+2 Profil

icon Re: Matematička indukcija09.06.2003. u 01:38 - pre 259 meseci
Možda pokušati naći neki pattern?
n=1 f(n)=1
n=2 f(n)=2
n=3 f(n)=5
n=4 f(n)=14
n=5 f(n)=42
n=6 f(n)=132
n=7 f(n)=429
n=8 f(n)=1430
n=9 f(n)=4862
n=10 f(n)=16796

Nadam se da je ovo tačno. Kod mat. indukcije takođe može biti slučaj da u drugom koraku pretpostavimo da je tvrdnja tačna za k<=n, pa da onda dokazujemo za k=n+1.

Iz gornjeg mi se čini da f(n)/(n+2) nije prirodan broj

Pozdrav svima i hvala što postujete na ovu temu.
 
Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
*.ptt.yu



+64 Profil

icon Re: Matematička indukcija09.06.2003. u 09:41 - pre 259 meseci
Ima tu još i dvojka koja može da pomogne.
2n+1 ne može, jer je

a što je ceo broj samo za n=1, pa ne pomaže mnogo...

moderator: sređen kod.

[Ovu poruku je menjao tOwk dana 10.06.2003. u 18:35 GMT]
 
Odgovor na temu

pixelmania
Marko Jovanović
Beograd

Član broj: 3766
Poruke: 129
*.199.EUnet.yu

ICQ: 113685276
Sajt: www.pixelmania.go.to


Profil

icon Re: Matematička indukcija10.06.2003. u 23:41 - pre 259 meseci
E, a ko kaže da

mora da bude ceo broj?

Mislim ako je P(n) ceo broj, to znači samo da (n+1)(n+2) mora da deli P(n)
coito ergo sum - Marko Jovanović
 
Odgovor na temu

tOwk
Danilo Šegan
Zemun/Beograd

Član broj: 94
Poruke: 2743
*.beograd-3.tehnicom.net

ICQ: 9344053
Sajt: alas.matf.bg.ac.yu/~mm011..


+2 Profil

icon Re: Matematička indukcija10.06.2003. u 23:54 - pre 259 meseci
Taj „savet“ je dat još ranije (samo nešto jednostavnije, pošto ).

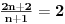
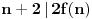
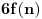
I u tom kontekstu su i mene već ispravili, pa „samo“ treba da . Čak, čini mi se da se može dobiti i razdvajanjem razlomka na dva dela (kako je već opisano).
Možda se moje mišljenje promenilo, ali ne i činjenica da sam u pravu.
 
Odgovor na temu

Mihailo Kolundzija
Novi Sad

Član broj: 11323
Poruke: 100
*.ftn.ns.ac.yu



+1 Profil

icon Re: Matematička indukcija16.06.2003. u 02:47 - pre 259 meseci
Probaj da resis sledeci zadatak:
Imas dve osobe - osoba A koja stoji na tacki (1, 0) i osoba B koja stoji na tacki (0, 1). Njihov cilj je da stignu u tacku (n+1, n) krecuci se samo "gore" i "desno", koracima duzine 1. Ti treba da nadjes razliku izmedju broja razlicitih puteva koji su na raspolaganju osobi A i broja razlicitih puteva koje moze da odabere osoba B. Kad resis ovaj zadatak, cuces odgovor na svoj zadatak.
 
Odgovor na temu

IdeaR
BiH

Član broj: 11048
Poruke: 126
*.as54.tz-old.bih.net.ba



+2 Profil

icon Re: Matematička indukcija18.06.2003. u 20:39 - pre 259 meseci
Hah! Izvanredan 'hint'! Da, zaista se dobije:



tj,



odnosno



Pošto je broj kombinacija bez ponavljanja prirodan broj, to je i razlika takva dva broja prirodan broj (jer se dobije pozitivna veličina). Čini mi se da je time zadatak dokazan? (nisam dokazivao da je broj kombinacija bez ponavljanja prirodan broj) Samo me buni, gdje se tu koristi mat. indukcija. Možda su autori zbirke imali neko drugo rješenje u vidu?
Pozivam daljnje komentare.

Opet puno pozdrava svima, a veliko hvala gosp. Kolundziji - super.
 
Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
*.ptt.yu



+64 Profil

icon Re: Matematička indukcija19.06.2003. u 08:42 - pre 259 meseci
Samo mala ispravka : drugi red nije u redu, jer je gore 2(n-1) = 2n-2.
A ono poslednje i nije potrebno.
U svakom slučaju nije za indukciju, mada može i tako.
 
Odgovor na temu

IdeaR
BiH

Član broj: 11048
Poruke: 126
*.as54.tz.bih.net.ba.



+2 Profil

icon Re: Matematička indukcija19.06.2003. u 19:53 - pre 259 meseci
Molio bih sve one koji imaju još ideja za rješenje zadatka, da ih napišu. Moj prethodni post jeste tačan (uredu je 2. red), ali mi je glupo da se rješenje zasniva na prilično nevjerovatnoj intuiciji ili iskustvu sa zadatkom sa sličnim rješenjem. Autori ove odlične zbirke ne bi dali taj zadatak u oblasti mat. indukcije tek onako?

Pozdravi svima!
 
Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
*.ptt.yu



+64 Profil

icon Re: Matematička indukcija20.06.2003. u 09:35 - pre 259 meseci
Hm da, izgleda da zaista jeste... sorry. Mislio sam da si to jednostavno dobio tako što si u prethodnom zamenio n sa n-1, kao što izgleda da je urađeno na desnoj strani? To mi je izgledalo najjednostavnije, a neko posebno dokazivanje za nešto drugo suvišno, jer tebe interesuje samo da napraviš pozitivnu razliku dva prirodna broja. Ali kada je to već učinjeno, zar nije tu kraj? Jedino ako želiš sledeći red da iskoristiš u indukciji. Mada je nacimavanje na indukciju malo bezveze kad već postoji ovakvo rešenje (veži konja gde ti gazda kaže ;).
 
Odgovor na temu

IdeaR
BiH

Član broj: 11048
Poruke: 126
*.as54.tz.bih.net.ba.



+2 Profil

icon Re: Matematička indukcija20.06.2003. u 20:44 - pre 259 meseci
Da, tu jeste kraj.
Ali me interesuje i rješenje putem mat. indukcije koje vjerovatno nema veze sa ovim gore. Ali, eto, da ne bi bio dosadan, neću to više spominjati poslije ovog posta.

Pozdravi
 
Odgovor na temu

Mihailo Kolundzija
Novi Sad

Član broj: 11323
Poruke: 100
*.ftn.ns.ac.yu



+1 Profil

icon Re: Matematička indukcija20.06.2003. u 21:34 - pre 259 meseci
Ja sam pokušao da kažem da je , ali vidim da si našao i drugi način.
Ako baš hoćeš da se bakćeš sa indukcijom, probaj ovako:

U brojiocu i imeniocu imaš proizvod od (n-2) uzastopna prirodna broja (još u brojiocu imaš i onu trojku ako ti zatreba), i treba da dokažeš da je taj razlomak ceo broj.
 
Odgovor na temu

IdeaR
BiH

Član broj: 11048
Poruke: 126
*.as54.tz.bih.net.ba.



+2 Profil

icon Re: Matematička indukcija21.06.2003. u 02:01 - pre 259 meseci
Hmmm:). Moj 'drugi' način je tekao ovako:
Broj različitih puteva za A:

a za B:


Pošto nisam krenuo odmah tražiti zbirove članova svakog reda pojedinačno (što bi bio logičan korak:)), prvo sam oduzeo A-B, i dobio:



valjda nadajući se da ću u tom koraku izbjeći traženje sume redova A i B, što sam očito morao svejedno uraditi. Odatle gornji izraz.

Puno pozdrava
 
Odgovor na temu

[es] :: Matematika :: Matematička indukcija

[ Pregleda: 11394 | Odgovora: 17 ] > FB > Twit

Postavi temu Odgovori

Srodne teme
Navigacija
Lista poslednjih: 16, 32, 64, 128 poruka.