• Naslovna
• FAQ
• Pravilnik
• O ES-u
• Tim
• Korisnici
• Statistike

 

• elitesecurity ::
• elitemadzone ::
• EMAIL ::
• RSS ::
• ES Mobile

  Niste ulogovani?  Username :   Password:   

• Registracija
• Zaboravili ste password?
• Flashback ▲▼
• Login problem?

 

Pretraga:

 

Srodne teme 27.06.2001. alternativa funkciji scanf() 30.09.2003. Pomoc - Matematicka Indukcija 16.02.2005. Indukcija 27.06.2004. slanje linka u mail funkciji 28.08.2004. WM_TIMER u thread funkciji kreiranoj sa CreateThr.. 03.03.2005. Indukcija i samoindukcija 25.06.2005. Broj trenutno aktivnih sesija na IIS-u u ASP-net-.. 22.08.2005. Patch-iranje servisa koji su u funkciji 16.02.2006. Ekvivalent Shell funkciji 22.02.2006. TStringList - exception safe ili ne? Navigacija Nedavno pregledane stranice:[es] - Indukcija na rekurzivnoj funkciji..[es] - TV-beko griju se zavojnice u mrez.. Brisanje liste Aktuelne teme u ovom forumu: Još jedan zadatak sa uglovima Treći zadatak sa uglovima Ostala rešenja algebarske jednačine Lep zadatak sa uglovima Najmanje pozitivno realno r Ikosaedar i gustina ms matematika.... Jedan zadatak sa pravouglim trouglom Japanese | Can you solve this ? | Math.. Jednakostraničan trougao Logaritamska nejednakost Raspoređivanje slova Košarkaši lep zadatak Zanimljiv zadatak o uglovima trougla Stado Boga Sunca ... 2000 godina star .. Izaberite forum: Linux Linux aplikacije Linux desktop okruženja Linux hardware Windows desktop Windows aplikacije Zaštita Office Windows drajveri Office :: Word Office :: Excel Macintosh Mac hardware Mac software Iphone Enterprise Networking SOHO Networking Wireless Windows mreže Linux mreže Wireless :: WiMax Wireless :: Mikrotik Wireless :: Wireless oprema Linux/UNIX serveri i servisi Unix BSD Skript jezici Security Virtualizacija Cloud Computing Services Security :: Kriptografija i enkripcija .NET 3D programiranje Art of Programming Asembler C/C++ programiranje Kernel i OS programiranje Pascal / Delphi / Kylix Java Embedded sistemi Perl PHP Python Visual Basic 6 Veštačka inteligencija Security Coding XML GameDev - Razvoj Igara Ostali programski jezici PHP :: PHP za početnike PHP :: Smarty template engine .NET :: .NET Desktop razvoj .NET :: ASP.NET .NET :: WPF Programiranje C/C++ programiranje :: C/C++ za početnike Baze podataka MySQL Oracle Access MS SQL Firebird/Interbase PostgreSQL Fiksna telefonija VoIP Udruženje korisnika teleko.. GSM - telefoni GSM - upotreba GSM - servisiranje Mreže i novosti Smartphone Mreže i novosti :: Mobilni internet Mreže i novosti :: Telenor - korisnički servis Mreže i novosti :: VIP - korisnički servis Mreže i novosti :: MTS - korisnički servis Smartphone :: Symbian OS Smartphone :: Windows Mobile Smartphone :: Android GSM - telefoni :: Nokia PDA Uređaji GPS Portable Players Anonimnost i privatnost ISP Browseri E-mail Instant Messaging FTP Google Hosting ISP :: Wireless mreže i ISP ISP :: ADSL E-mail :: Anti-spam Instant Messaging :: IRC Hosting :: Domeni Google :: Gmail E-Marketing Web aplikacije Web dizajn i CSS Web dizajn softver Web razvoj Pretraživači i SEO Flash Javascript i AJAX Web dizajn i CSS :: Kritike Grafički dizajn Izdavaštvo 3D modelovanje Rasterska grafika Vektorska grafika 3D modelovanje :: CAD/CAM Matične ploče, procesori .. Video karte i monitori Storage Ostali hardver Overclocking & Modding PC Konfiguracije Laptopovi Vodič za kupovinu - PC har.. Tablet PC Muzička produkcija Audio kompresija Audio softver Video produkcija Video kompresija Video softver Multimedijalni uređaji Digitalni fotoaparati Digitalne kamere Home Theater Digitalni fotoaparati :: Fotografija Digitalni fotoaparati :: Vodič za kupovinu - Digita.. Elektronika Elektrotehnika Elektronika :: TV uređaji Elektronika :: Radio elektronika i tehnika Elektronika :: Mikrokontroleri Elektronika :: Audio-elektronika Auto-elektronika :: Tuning Vodič za učenje Vodič za posao Vodič za emigraciju Fizika Matematika Nauka Sertifikati Informatika Vodič za učenje :: Seminarski radovi Vodič za učenje :: Obrazovne institucije Vodič za emigraciju :: Život u USA Vodič za emigraciju :: Život u Norveškoj Vodič za emigraciju :: Život u Nemačkoj E-Poslovanje E-Kupovina IT pravo i politika razvoja IT događaji IT berza poslova IS i ERP Ekonomija Berza Cryptocoins IT berza poslova :: Arhiva IT berze poslova IT pravo i politika razvoja :: Registar Nacionalnog ID E-Poslovanje :: E-Transakcije E-Poslovanje :: Forex E-Kupovina :: Platne kartice Digitalna Televizija Advocacy Ankete Predlozi i pitanja Vesti Čekaonica Vesti :: ES leto manifestacija MadZone TechZone Poljoprivreda AutoZone MotoZone Svakodnevnica Video igre MadZone :: Zanimljivi linkovi MadZone :: Kultura TechZone :: Ergonomija TechZone :: Grejanje TechZone :: Klimatizacija TechZone :: Bela tehnika AutoZone :: Fiat Panda club Lista poslednjih: 16, 32, 64, 128 poruka.

bags Član broj: 10072 Poruke: 715 *.12.15.tuwien.teleweb.at +2 Profil Indukcija na rekurzivnoj funkciji 07.03.2004. u 18:57 - pre 257 meseci Moze li mi neko pomoći oko ovog zadatka : Pokazati pomoći matematičke indukcije ,da za rekurzivno definisanu funkciju : 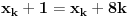za svako k =>1 važi 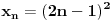za svako n => 1 . Zadatke kada su dati nizovi preko opšteg člana znam riješavati,ali ovo mi je prvi ovakav ,a nemam primera ni u skripti ni u knjizi,pa ako bi neko mogao da da smjernice bio bih zahvalan. Free advice is seldom cheap. Odgovor na temu

noviKorisnik Dejan Katašić Novi Sad Član broj: 13216 Poruke: 4533 *.neobee.net Sajt: www.novikorisnik.net +5 Profil Re: Indukcija na rekurzivnoj funkciji 07.03.2004. u 21:44 - pre 257 meseci Fali ti početni uslov, koliko je x1? Pošto se traži dokaz putem indukcije, verovatno nije predviđeno da dođe do pucanja pri prvom koraku, tako da bih rekao da je x1 = 1. Sada klasična indukcija: Korak 1: k=1: x1 + 1 = x1 + 8*1 x2 = 1 + 8 = 9 proverimo da li zadovoljava: x2 = (2*2 - 1)2 = 9. OK Korak 2: pretpostavka: za k = n-1 važi xn = xn - 1 + 8(n - 1) = (2n - 1)2 Korak 3: k = n Znamo: xn + 1 = xn + 8n Treba pokazati: xn + 1 = (2(n + 1) - 1)2 ... to pokušaj već sam. Zadatak se i svodi na to da dokažeš da zadani rekurzivni oblik člana niza ima opšti član jednak drugom izrazu. BoxUp interesantna logička igra Monty Hall paradoks - interaktivni demo Odgovor na temu

bags Član broj: 10072 Poruke: 715 *.12.15.tuwien.teleweb.at +2 Profil Re: Indukcija na rekurzivnoj funkciji 09.03.2004. u 13:38 - pre 257 meseci Hvala što si napisao fino cijeli postupak. Dalje je bilo stvarno lako. :) Free advice is seldom cheap. Odgovor na temu