Apsena sam pročitao u školi (sva četiri toma zajedno sa zbirkama) i tada mi je bio koristan, ali za ozbiljniji matiš to nije.
Recimo, kada govori o totalnom diferencijalu, daje teoremu po kojoj je izraz
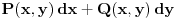
totalni diferencijal neke funkcije ako i samo ako je
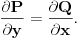
Pritom, ne navodi nikakve dodatne uslove, kao na primer da se sve razmatra na domenu koji je otvoren skup (recimo, oblast), da navedeni parcijalni izvodi postoje (neka bude da se to podrazumeva) niti da su ti parcijalni izvodi neprekidni.
Štaviše, navodi i neki dokaz te teoreme u kome vrši diferenciranje integrala po parametru, potpuno opušteno, bez ikakve provere da li je to u tom slučaju dozvoljeno ili ne. Nekada se na matematičkom fakultetu dobijalo 0 (i slovima nula) bodova za takva rešenje. Inače, to nisu matematičari bezveze izmislili, već postoje slučajevi kada diferenciranje integrala po nekom parametru nije dozvoljeno. Recimo, rešenje Puasonove parcijalne diferencijalne jednačine (koja ima važno mesto u fizici) se izražava preko integrala gde je diferenciranje po parametru (koji je zapravo bilo koja od nepoznatih) dozvoljeno jedanput, ali ne i dvaput. Kada bi moglo, sve bi propalo. Rešenje se zasniva upravo na tome da drugi put ne može da se formalno diferencira po parametru.
To je kao kada bi iz pretpostavki da dva trougla imaju podudaran par uglova, podudaran par stranica nasuprot tih uglova i još jedan podudaran par stranica zaključio da su ta dva trougla podudarna (kao što je to činio Vene Bogoslavov u zbirkama za srednju školu). To jeste tačno uz još neke uslove (recimo da nije jedan od tih trouglova pravougli, a drugi tupougli).
U teoriji je Apsen išao na to da da formule, bez navođenja uslova pod kojima one važe. U zbirkama je nastojao da da recepte za računanje. Međutim, sve je to nekako bilo bez razumevanja. Nešto kao kada bi naučio kako se računaju integrali kao što je
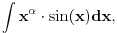
a onda sa integralima tipa
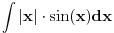
ili
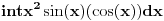
mogao da se slikaš zbog nedostatka razumevanja mateije naučene na taj način.
Da ne tupim više. Smatram da je Apsen dobar za naprednije gimnazijalce koji žele da prošire svoje znanje, ali ne i za nešto ozbiljnije od toga.
[Ovu poruku je menjao Nedeljko dana 30.12.2006. u 02:12 GMT+1]
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
Najbolja zbirka iz Matematike I
Re: Najbolja zbirka iz Matematike I
Re: Najbolja zbirka iz Matematike I
Re: Najbolja zbirka iz Matematike I