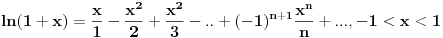Verujem da ti je jasno zašto je
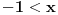
, pogledajmo zašto mora da bude i
.
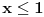
Za svaki slučaj napisaću i definiciju
Maklorenovog polinoma stepena
za neku datu
puta diferencijabilnu f-ju
:
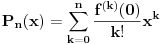
, pri čemu je
-ti izvod f-je
obeležen sa
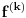
(po definiciji se uzima da je
).
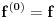
Greška (kaže se i ostatak) aproksimacije f-je
Maklorenovim polinomom
-tog stepena u tački
je
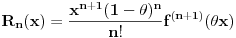
, za neko
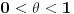
. (naravno f-ja mora da bude
puta diferencijabilna)
Lako je proveriti da je za
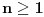
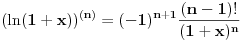
, otuda imamo da je
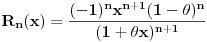
za neko pogodno odabrano
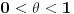
Dakle, za svako
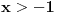
postoji
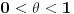
, tako da je
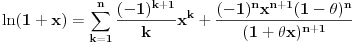
E sad nama je u interesu da ona greška aproksimacije teži nuli kad
teži beskonačnosti, međutim ispostavilo se da to nije moguće za svako
.
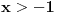
Sad bi bio zgodan trenutak da se prisetimo da
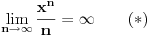
pod uslovom da je
.
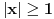
Pošto je
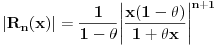
dovoljno je da ispitamo kada je
.
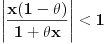
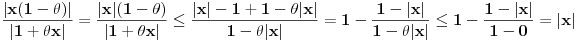
(u proceni je upotrebljena nejednakost
)
Znači, za
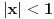
ostatak teži nuli.
A ako je
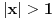
, onda opšti član reda ne teži nuli (to je na osnovu primedbe
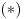
) pa je red divergentan.
Slučaj kada je
se jednostavno proverava (ostatak teži nuli).
Nadam se da je ovim otklonjena svaka sumnja u vezi sa intervalom - ostaje još samo da se neko smiluje pa da ti prekuca sam dokaz
Tejlorove teoreme - mene u ovom momentu nešto mrzi - jer sam siguran da ga možeš naći u svakom standardnom udžbeniku iz
Analize 1 (ima i dosta besplatnih e-knjiga na netu u kojima se to može naći). Ako se baš nikako ne snađeš - javi pa ću ti prekucati ceo dokaz.
Inače, rešenje koje ti je odmah dao
Farenhajt je potpuno korektno. Naime postoji teorema koja kaže da ako je npr. red
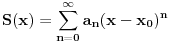
kovergentan u nekom radijusu konvergencije
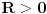
, onda se unutar tog radijusa konvergencije može diferencirati član po član tj.
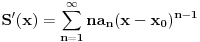
a dobijeni red imaće isti radijus konvergencije
.
Treba samo primetiti da je u datom slučaju
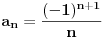
pa je
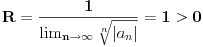
(jer je
).
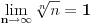
Dokaz te teoreme počiva ne nekim drugim jednostavnim stavovima, ali je stvarno glomazno da ti sad kucam sve neophodne definicije i leme.
Takođe moguće je uz pomoć jedne druge teoreme pokazati da jednakost važi i za
.
Za slučaj da ti nije jasan ni formalni deo
Farenhajtovog rešenja, da prepričam: uzimamo da je
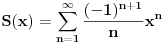
, ispostavi se da je
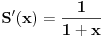
, zapitamo se kakvo mora biti
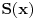
da bi imalo takav izvod, preko integrala dobijemo odgovor:
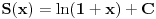
a pošto iz definicione jednakosti sledi da je
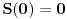
, onda mora biti i
.
Na kraju, imam samo jednu molbu, da ako se desi (a već se dešavalo) da ti je neki korak sumnjiv da precizno ukažeš o čemu se radi - potpuno mi je jasno da ti već imaš neka očekivanja kako bi dokaz morao da izgleda (u smislu da ispuni neke standarde) i onda u "žaru matematičke borbe" lako zaboraviš da je neko možda uložio dosta svog slobodnog vremena u pokušaju da ti pomogne - pa ako se i desi da je pogrešio ili da ti je neki detalj sumnjiv, treba na to vrlo precizno i pažljivo skrenuti pažnju.
Edit: Umesto ostatka u
Lagranžovom obliku koji je prvobitno bio napisan, sada stoji ostatak u
Košijevom obliku - sve to u cilju "krpljenja" rupe u jednom delu dokaza.
[Ovu poruku je menjao uranium dana 24.02.2006. u 15:28 GMT+1]
Attempt all the problems. Those you can do, don't do. Do the ones you cannot.
Tejlorov red-zadatak
Registrovani: 6 ( eeestablishment, valjan, quujabaar, Biske01, Andra_Ivic, djoka_l )
), ali pošto se ono 
