• Naslovna
• FAQ
• Pravilnik
• O ES-u
• Tim
• Korisnici
• Statistike
• Jabber
• Email
• Chat
• Posao

• elitesecurity ::
• elitemadzone ::
• WAP ::
• EMAIL ::
• NEWS ::
• RSS

  Niste ulogovani?  Username :   Password:   

• Registracija
• Izgubili ste password?
• Flashback ▲▼

Pretraga:  

Srodne teme 17.08.2002. Integral 07.11.2003. Kod DOS interrupt-a 26.01.2004. Nesvojstveni integral - deliti ili ne? 06.06.2004. problem povezivnja dva uslova kod filtriranja baze 15.09.2004. premotavanje divx filmova kod skyvision-a 09.09.2004. Dvojba oko rijesenja Integrala ln (x) 26.05.2005. digest funkcija kod mejla 16.11.2005. Izbor teme maturskog rada-zelim samo savjet 09.01.2006. Problem sa neodredjenim integralom - metoda smene Navigacija Brisanje liste Aktuelne teme u ovom forumu: pomozite da rijesimo Sistemi linearnih jednacina Rutinski problemi - objašnjenje,suges.. pomozite da rijesimo max povrsina pravougaonika Delta distribucija parcijalne diferencijalne jednacine u .. Dualni prostor pojasnjenje Permutacije, pomoc Ispitivanje sličnosti iz Osnova geome.. on-line matematicki recnik? potrebna pomoc hitno pomozite da rijesimo pomozite mi imam problem Dva zadatka iz linearne algebre - pomoc Izaberite forum: Linux Linux aplikacije Linux desktop okruženja Linux hardware Windows desktop Windows aplikacije Zaštita Office Windows drajveri Windows aplikacije :: Browseri Office :: Word Office :: Excel Macintosh Mac hardware Mac software Enterprise Networking Home Networking Wireless Windows mreže Linux mreže Wireless :: WiMax Wireless :: Mikrotik Wireless :: Wireless oprema Linux/UNIX serveri i servisi Unix BSD Skript jezici .NET 3D programiranje Art of Programming Asembler C programiranje C++ programiranje Kernel i OS programiranje Pascal / Delphi / Kylix Java Embedded sistemi Perl PHP Advanced PHP Python & Zope Visual Basic 6 Veštačka inteligencija XML GameDev - Razvoj Igara Ostali programski jezici C programiranje :: C za početnike PHP :: Smarty template engine .NET :: .NET Desktop razvoj .NET :: ASP.NET .NET :: .NET Presentation Foundation C++ programiranje :: C++ za početnike Baze podataka MySQL Oracle Access MS SQL Firebird/Interbase PostgreSQL Kriptografija i enkripcija Security Security Coding Fiksna telefonija VoIP Udruženje korisnika teleko.. GSM - tržište GSM - upotreba GSM - servisiranje Mreže i novosti Smartphone Mreže i novosti :: GPRS Mreže i novosti :: Telenor - korisnički servis Mreže i novosti :: VIP - korisnički servis Mreže i novosti :: MTS - korisnički servis Smartphone :: Symbian OS Smartphone :: Windows Mobile GSM - tržište :: Nokia GSM - tržište :: Samsung GSM - tržište :: Siemens GSM - tržište :: SonyEricsson GSM - tržište :: Motorola GSM - tržište :: LG PDA Uređaji GPS Portable Players Anonimnost i privatnost ISP E-mail File Sharing Instant Messaging FTP Google Hosting ISP :: Wireless mreže i ISP ISP :: ADSL E-mail :: Anti-spam Instant Messaging :: IRC Instant Messaging :: Jabber i XMPP Hosting :: Domeni Google :: Gmail E-Marketing Web aplikacije Web dizajn i CSS Web dizajn softver Web razvoj Pretraživači i SEO Flash Javascript i AJAX Web dizajn i CSS :: Kritike E-Marketing :: Affiliate Programi Grafički dizajn Izdavaštvo 3D modelovanje Rasterska grafika Vektorska grafika 3D modelovanje :: CAD/CAM Matične ploče, procesori .. Video karte i monitori Storage Ostali hardver Overclocking & Modding PC Konfiguracije Laptopovi Muzička produkcija Audio kompresija Audio softver Video produkcija Video kompresija Video softver Multimedijalni uređaji Digitalni foto-aparati Digitalne kamere Digitalni foto-aparati :: Fotografija Elektronika Elektronika :: TV uređaji Elektronika :: Radio elektronika i tehnika Elektronika :: Mikrokontroleri Elektronika :: Audio-elektronika Auto-elektronika :: Tuning Vodič za učenje Vodič za posao Vodič za emigraciju Fizika Matematika Nauka Sertifikati Vodič za učenje :: Seminarski radovi Vodič za učenje :: Obrazovne institucije E-Poslovanje E-Kupovina IT pravo i politika razvoja IT događaji IT berza poslova IS i ERP Berza IT berza poslova :: Arhiva IT berze poslova IT pravo i politika razvoja :: Registar Nacionalnog ID E-Poslovanje :: E-Transakcije E-Poslovanje :: Forex E-Kupovina :: Platne kartice BalkanSat BalkanSat :: Dreambox,Samsung,Humax,D-box BalkanSat :: PC DVB kartice Advocacy Ankete Predlozi i pitanja Vesti Čekaonica Vesti :: ES leto manifestacija MadZone TechZone MadZone :: Zanimljivi linkovi TechZone :: Ergonomija TechZone :: Klimatizacija i bela tehnika TechZone :: AutoZone Lista poslednjih: 16, 32, 64, 128 poruka.

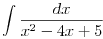
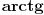
Tisma Miroslav Tišma Lazarevac Član broj: 13213 Poruke: 293 212.62.51.* Jabber: tisma@elitesecurity.org ICQ: 178671901 Profil Smena kod integrala racionalnih funkcija 20.02.2006. u 23:34 Zbunjuje me to što se kod ovakvih integrala koji se svode na tablične - praktično možemo pisati u imeniocu onaj binom na dva načina, kao 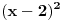ili kao 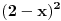, a diferencijal od 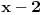i 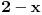nije isti već se razlikuje u znaku! U zbirkama je samo rešenje 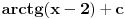.Može li neko da mi objasni ovo i da mi napiše rešenje za ovaj integral? Bolje jedno vruće pivo nego četri ladna! 20.02.2006. u 23:34

peddja_stankovic predrag stankovic beograd Član broj: 48085 Poruke: 160 *.r62.logikom.net. Sajt: www.geocities.com/predrag.. Profil Re: Smena kod integrala racionalnih funkcija 20.02.2006. u 23:42 Ako stavis smenu x-2 dobijas upravo taj rezultat koji si naveo arctg(x-2)+c Ako stavis smenu 2-x rezultat dt=-dx pa je resenje -arctg(2-x)+c a to ti je isto sto i arctg(x-2)+c jer je arctg neparna funkcija, tako da nema nikakvog paradoksa [Ovu poruku je menjao peddja_stankovic dana 21.02.2006. u 07:27 GMT+1] Ne znam kako mi to uspeva, ali znam da mi uspeva 20.02.2006. u 23:42

Tisma Miroslav Tišma Lazarevac Član broj: 13213 Poruke: 293 212.62.51.* Jabber: tisma@elitesecurity.org ICQ: 178671901 Profil Re: Smena kod integrala racionalnih funkcija 21.02.2006. u 22:26 To mi je i profesorka danas rekla. Ja to nisam uzeo u obzir, pa me je bunilo. U svakom slučaju hvala na objašnjenju. Bolje jedno vruće pivo nego četri ladna! 21.02.2006. u 22:26