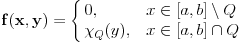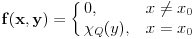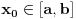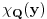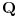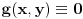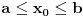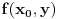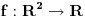 integrabilna na pravougaoniku
integrabilna na pravougaoniku 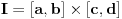
Fubinijeva teorema kaze da je
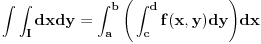
Medjutim, iako je f integrabilna na I, integral po [c, d] funkcije f(x, y) za fiksirano x uopste ne mora da postoji.
Jel moze neko da mi kaze zasto, ili jos bolje, primer kad ne postoji
Hvala




 Fubinijeva teorema
Fubinijeva teorema