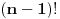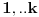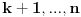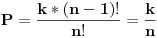Kad se desi dogadjaj A izvucena je 10-ta kuglice koja je boje x,nakon 9 cnih,dese se i sledeci dogadjaji:
A1.Izvucen je niz od jedne crne i druge x.(prethodno se racuna kao prvo)
A2.Izvucen je niz od 2 crne i jedne x.
...
A10.Izvucen je niz od 9 crnih i jedne x.
(idemo dalje u proslost)
A11.Izvucen je niz od jedne boje y1,9 crnih i jedna x.
A12.Izvucen je niz od dve,boja y2 i y1,9 crnih i jedna x.
...
(idemo u proslost do prvog izvlacenja,jer otkud mi znamo da li je anse izvlacenje prve crne bilo prvo ili je neko pre bnas izvlacio.)
U ovoj "levoj pololovini" vremena,desili su se i osali nizovi gogadjaja,npr.izvucna je y2 i y1 zaredom(kad posmatramo asmo njih isl.)
Dakle imamo skup svih podintervala od slupa izvlacenja,gde je skup izvlacenja (s leva) najvise prebrojiv.
Posto P(A) racuna kao ad je A nezavisan,od 9 crnih kuglica pre,a tako i svaki P(Ai),a ocigledno je ad recimo P(A2) stoji u nekom odnosu sa P(A),nisu nezavisni,i ocigledno je da ako se desi P(A) desi se i P(A1) i jos neki...
PITANJE JE Da li je P(A)= P(ΣAi : Ai ima izvucen x tamo gde smo ga mi izvukli)
Ili da li dogadjaj A ima ver. kao ver da se desi bar jedan od nizova Ai,koji sadrzi kuglicu x na tacnom mestu?
Pri cemu smo definisali neka mesta kao fiksno odredjena(npr. crne kuglice)
Ili slican problem.
Dat je niz a1 a2 ... ak ...an. ai iz {0.1} belo-crno
Definisano je a[k-9] do a[k-1]=1 (nase crne kugle)
Svi ostali se popunjavaju slucajno bez varanja.
Definisemo P(a
...a[i+j]=y1,y2,...yj)
P(a...a[i+j]=y1...yj)=F(λ,P((ak,...a[k+l])=yk,...y[k+l] ) gde postoji a[k+q]=a[i+r]) a lambda je ostatak zavisnosti,neka funkcijica koja ukljucje odnos duyina nizova,pozicija nizova isl.
Receno usmeno,nizovi koji se bar malo preklapaju imaju zavisne verovatnoce.Treba mi da u tom momentu izvlacenja 10-kuglice,svaka verovatnoca da se desi niz koji ce se izvlacenjem te kuglice boje x desiti,jednaka ver.da se desi sama ta kuglica.Jer ako bi bilo drugacije,onda ne bi bilo dobro?
Nemam sad vremena da precizno ali nadam se da shvatas ideju.
www.eden.rs
Izdavač duhovne i filozofske literature




 2 pitanja iz verovatnoce
2 pitanja iz verovatnoce Re: 2 pitanja iz verovatnoce
Re: 2 pitanja iz verovatnoce