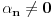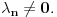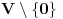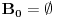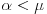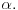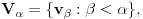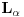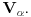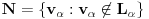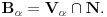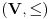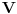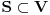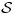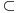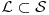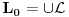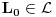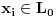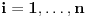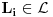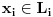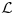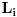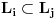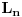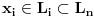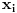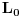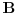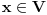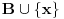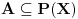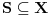Ja znam jedan malo drugaciji dokaz koji se u sustini svodi na isto, samo sto se koristi Zornova lema:
Ako je
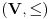
parcijalno uredjen skup i ako svaki lanac (skup elemenata tako da su svaka dva uporediva) ima gornju granicu, onda
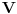
ima maksimalni element.
Uocis sve
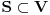
koji su linearno nezavisni. Skup svih takvih podskupova (
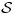
sa relacijom
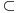
cini parcijalno uredjen skup, a ako je
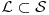
lanac, njegova gornja granica je
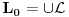
. Da bi to dokazali, dovoljno je da dokazemo da je
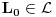
.
Zaista, ako su
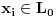
,
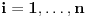
onda postoje skupovi
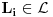
tako da je
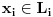
. Posto je
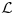
lanac, to su svaka dva skupa
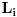
uporediva (tj ili je
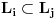
ili obrnuto), pa medju njima postoji najveci (tj onaj tako da su svi ostali njegovi podskupovi). Neka je to
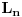
. Prema tome
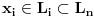
pa su
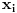
linearno nezavisni. Dalje sledi da je,
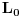
linearno nezavisan odnosno
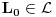
. Na osnovu Zornove leme sad sledi da postoji maksimalni element
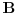
u
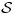
, i on je maksimalan linearno nezavisan skup (tj kad mu dodas bilo koji vektor prestaje da bude linearno nezavisan). Na osnovu trivijalne posledice da je max. lin. nez. sistem ujedno i minimalni potpun sledi da je
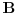
baza.
Posledica se dokazuje tako sto pretpostavis da je
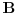
nepotpun, tj da postoji
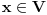
koji ne moze da se izrazi kao lin. kombinacija vektora iz
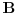
, onda uocis
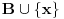
i za njega dokazes da je lin. nez. a to je kontradikcija jer je
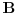
max. lin. nez.
Nadam se da sam ti pomog'o, tj da te nisam jos vise zbunio :). Inace, mnogim mojim kolegama sa faxa ova teorema je bila veliki problem, a verujem da ju je malo njih uopste skontalo :), nego su isli na onu varijantu a valjda nece da mi se padne ili profesor to retko pita :)!
ps. Ovaj dokaz je iz knjige Lj. Kocinac: Linearna algebra i analiticka geometrija
DeXteR[ity]!!!!
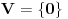 tada je baza
tada je baza 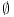 .
.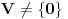 tada koristimo Zermelov princip dobrog uredjenja na osnovu koga se skup (nosač vektorskog prostora) predstavlja u obliku koji je izomorfan nekom ordinalu
tada koristimo Zermelov princip dobrog uredjenja na osnovu koga se skup (nosač vektorskog prostora) predstavlja u obliku koji je izomorfan nekom ordinalu  , tj.
, tj. 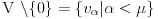 , pa dalje kaže:
, pa dalje kaže: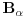 :
: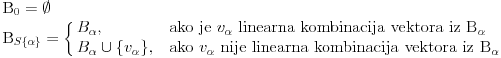
 granični :
granični : 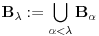
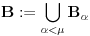 .Tvrdimo da je
.Tvrdimo da je  baza.
baza. je generatrisa :
je generatrisa :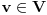 , tada je
, tada je 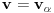 za neko
za neko 
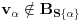 , što znači da je
, što znači da je 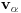 linearna kombinacija vektora iz
linearna kombinacija vektora iz 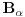 pa time i
pa time i  .
.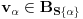 , što znači da je
, što znači da je 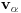 iz
iz  .
. je linearno nezavisan:
je linearno nezavisan: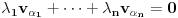 linearna kombinacija vektora iz
linearna kombinacija vektora iz  , tj.
, tj. 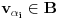 . Neka je
. Neka je 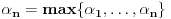 i neka je
i neka je 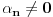 .
.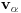 linearna kombinacija (manjih) nekih vektora za
linearna kombinacija (manjih) nekih vektora za 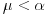 pa po konstrukciji
pa po konstrukciji 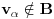 , što je kontradikcija.
, što je kontradikcija.



 Zermelov princip dobrog uredjenja i dokaz da svaki vektorski prostor ima bazu
Zermelov princip dobrog uredjenja i dokaz da svaki vektorski prostor ima bazu