Srodne teme
Navigacija
Lista poslednjih: 16, 32, 64, 128 poruka.

Pomoc u vezi sume kvadrata

[es] :: Matematika :: Pomoc u vezi sume kvadrata

[ Pregleda: 1277 | Odgovora: 7 ]

 Postavi temu Odgovori

Autor
Pretraga teme: Traži
Markiranje Štampanje RSS

sMRDo
560012548
Graz

Član broj: 56428
Poruke: 60
*.vc-graz.ac.at.



Profil

icon Pomoc u vezi sume kvadrata09.05.2005. u 16:44

Zna li neko kako glasi suma kvadrata za izraz : ((x^2 + x + 1))^2
09.05.2005. u 16:44 

sMRDo
560012548
Graz

Član broj: 56428
Poruke: 60
*.vc-graz.ac.at.



Profil

icon Re: Pomoc u vezi sume kvadrata09.05.2005. u 18:50
Vidim da svi gledaju a niko ne odgovara. Potezak problem da se ovo sve svede u jedan opsti oblik zar ne ???
09.05.2005. u 18:50 

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 813
*.dialup.blic.net.



Profil

icon Re: Pomoc u vezi sume kvadrata09.05.2005. u 22:51
Da nisi ti zalutao ovdje?Šta ti je tu x?Odakle dokle da pravimo sumu?
Citat:
sMRDo: Zna li neko kako glasi suma kvadrata za izraz : ((x^2 + x + 1))^2

Ja bih znao naći sumu,ako je x prirodan broj i nije veći od 2.To je onda:

S=58
Jesam li pogodio?
09.05.2005. u 22:51 

KPYU
Karan Predrag

Član broj: 36769
Poruke: 143
*.dial.InfoSky.Net.



Profil

icon Re: Pomoc u vezi sume kvadrata10.05.2005. u 00:18
Da li hoćeš da pitaš koliko je ?

Pa to je

Ako ne želiš to da pitaš, hajde formuliši pitanje.
10.05.2005. u 00:18 

sMRDo
560012548
Graz

Član broj: 56428
Poruke: 60
*.vc-graz.ac.at.



Profil

icon Re: Pomoc u vezi sume kvadrata10.05.2005. u 01:15
Da KPYU to me je zanimalo

samo koje je to pravilo imali kakva formula za uopsteno izracunavanje takvih problema???

Koliko primjetim ide simetrija neka zar ne, 1 2 3 2 1 imali ko da mi da hint za rjesavanje ovakvih problema???

Hvala unaprijed
10.05.2005. u 01:15 

Djomloun
Mladjan Jovanovic
Bgd

Član broj: 3604
Poruke: 985
*.245.EUnet.yu.

ICQ: 158628304
Sajt: blogoye.org/djomlouns


Profil

icon Re: Pomoc u vezi sume kvadrata10.05.2005. u 09:12
Koliko se ja secam to se zove Pascalov trougao, i izgleda nekako ovako

n=0 1
n=1 1 2 1
n=2 1 3 3 1
n=3 1 4 6 4 1
n=4 1 5 10 10 5 1

i to je za koeficijente clanova, a za stepene, ide se prvi na n puta drugi na 0, pa seldeci je na n-1 puta drug na 0+1 ......... i sve do kraja kada je prvi na n-n=0 puta drugi na n (odnosno uvek je zbir stepena prvog i drugog clana proizvoda jednak n).
Inace ovo vazi kada imamo dva clana u zagradi.
Josx dok sam bio klinac baba me je uchila da ne jedem zxut sneg, citamo se na mojoj svasxtari lnk: http://blogoye.org/djomlouns/

ZM0501 :)


//napustio [es]...
10.05.2005. u 09:12 

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3501
*.dialup.neobee.net.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253


Profil

icon Re: Pomoc u vezi sume kvadrata10.05.2005. u 09:40
Ovo što je Djomloun pomenuo je binomna teorema, i kao što je rekao može se koristiti samo kada su u zagradi dva člana. Međutim, postoji uopštenje i sa više članova u zagradi, zove se multinomna teorema i nije naročito jednostavna, ali sam si tražio :)

Nadam se da sam jasno napisao, pokušaj na nekoliko primera pa ćeš videti kako to funkcioniše.
Ljubičice crvena, što si plava kô zelena trava.
10.05.2005. u 09:40 

KPYU
Karan Predrag

Član broj: 36769
Poruke: 143
62.108.101.*



Profil

icon Re: Pomoc u vezi sume kvadrata11.05.2005. u 00:55
Multinomni obrazac koji je napisao Bojan je sasvim tačan & cool, čak se formule za nj mogu naći u elementarnoj kombinatorici pod naslovom "Permutacije sa ponavljanjem", ali ....

Možda je lakše ako napišeš ovako



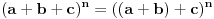
Čak bih rekao da je formulu za kvadrat, donekle i kub, zbira mnogo lakše kontaju tako što se nauče napamet.



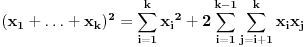
btw ovo nije suma kvadrata, nego kvadrat sume.
11.05.2005. u 00:55 

[es] :: Matematika :: Pomoc u vezi sume kvadrata

[ Pregleda: 1277 | Odgovora: 7 ]

 Postavi temu Odgovori

Srodne teme
Navigacija
Lista poslednjih: 16, 32, 64, 128 poruka.