Geometrijski zadatak sa JBMO 2005

Evo zadatka sa JBMO 2005.

(Rumunija) Dat je ostrougli trougao ABC. Tangenta u A kruga K(A,B,C) sece pravu BC u tacki D. Neka je M srediste duzi AD. Duz BM sece kruznicu k(A,B,C) u tacki R razlicitoj od B. Prava DR sece kruznicu k u tacki S razlicitoj od R. Dokazati da je CS paraleleno sa AD.



Malo ucenika je resilo ovaj zadatak ( 3-4 ) i to preko slicnosti. Kako za JBMO nije predvidjena slicnost zanima me da li neko moze da ga resi bez slicnosti?

Ja se trenutno mogu setiti tri rešenja koja ne zahtevaju sličnost, iako ne verujem da ih osnovci uopšte mogu razumeti qzqzqz je nestrpljiv pa ću napisati ono koje je najmanje nezanimljivo (preostala dva su kompleksni brojevi i trigonometrija pa koga ne mrzi neka računa).

Zahvaljujući projektivnoj geometriji dovoljno je pokazati da tvrđenje važi u tri proizvoljna slučaja. Uzmimo da je i odaberimo tri proizvoljne tačke . U tom slučaju se poklapa sa tangentom u pa tvrđenje očigledno važi.
Kraj zadatka, a nigde sličnosti :)

---

Bojane, sigurno ces me ispraviti ako gresim, ali u projektivnoj geometriji ne postoje pojmovi ostrog ugla, kruga, sredista duzi ni paralelnosti - po jedan iz skoro svake recenice zadatka. Stoga je ovakav tvoj pokusaj dokaza besmislen.

Osim toga, u bilo kojoj geometriji u kojoj imamo pojam "ostrouglog", cak ni po najslobodnijoj definiciji trougla, ne moze biti ostrougli onaj trougao u kojem se dva temena poklapaju.

Osim toga, tvoja tri slucaja su sve samo ne proizvoljna, u onom smislu proizvoljnosti koji se trazi. Sva tri su vrlo specificno izabrani degenerisani slucajevi. Mogao bih tako i ja da kazem "proizvoljne tacke A, B i C su kolinearne" i da dokazem pomocu ista ta tri "proizvoljna" slucaja koje si naveo.

Osim toga, nisam ubedjen da se inace stvari mogu dokazati takvom vrstom pristupa sa odredjenim brojem proizvoljnih slucajeva, ali tu je vrlo moguce da gresim, ima nesto u tome...

Ali siguran sam da si u pravu sto se tice dokaza preko kompleksnih brojeva i trigonometrije!


Dodatak: Odgovor koji sam napisao se doduse odnosio na prethodnu verziju tvoje poruke, ali i sa ovom modifikovanom i dalje stoji.

_{[Ovu poruku je menjao Vladimir P. Filipovic dana 19.09.2005. u 17:17 GMT+1]}

Odmah da kažem da sam pretpostavljao da će moja poruka izazvati dosta nejasnoća jer zaista deluje konfuzno to što sam napisao, ali u tom momentu nisam imao vremena da se bolje izrazim, što ču sad učiniti (što je detaljnije moguće).

Najpre malo definicija.

Pod pojmom projektivna prava podrazumevamo bilo koju od sledećih konfiguracija:
A) skup tačaka na datoj pravoj;
B) skup pravih kroz datu tačku;
C) skup tačaka na datoj konusnoj krivoj;
D) skup tangenti na datu konusnu krivu.
Elemente navedenih skupova obuhvatamo zajedničkim imenom projektivna tačka. U daljem tekstu pojmovi prava i tačka označavaće zapravo projektivnu pravu i projektivnu tačku, redom.

Kada u nekom geometrijskom problemu od promenljive (projektivne) tačke na nekoj fiksnoj (projektivnoj) pravoj konstruišemo jedinstvenu tačku na nekoj pravoj (može a ne mora biti ), koristeći samo projektivne operacije (konkretno, crtanje jedinstvene konusne krive kroz date tačke i presek dve konusne krive) onda se ovo naziva projektivna transformacija. Kada kažem "jedinstveno" to znači da ni u jednom koraku ne smemo proizvoljno birati neku vrednost već nove elemente moramo dobijati samo na osnovu već postojećih. Smatram da bismo dokazivanjem da ovakva vrsta transformacija zaista očuvava dvorazmeru otišli predaleko od teme, mada smo se i sad već poprilično udaljili ali nema veze, ovo su prilično korisne stvari i oni koji ih ne znaju bi trebali da ih pročitaju, dok dokaz nije bitan i (naravno) nema ga potrebe navoditi prilikom svake primene navedene tehnike.

E sad nazad na naš zadatak (pojmovi "prava" i "tačka" opet dobijaju svoja euklidska značenja). Prvo da napomenem da trougao iz zadatka uopšte ne mora biti oštrougli, pokazaću da tvrđenje važi za bilo kakav trougao. Definišimo transformaciju koja tangentu koja varira - konfiguracija D), preslikava u pravu - konfiguracija B). Zapravo, ispostavlja se da u brzini zaista jesam pogrešio u prvoj poruci jer su svi slučajevi koje sam pomenuo zapravo jedna ista transformacija, ali to nije bitno, sad radim kako treba a usput i objašnjavam detaljnije. Uzimamo sledeća tri slučaja (pre nego što krenem sa nabrajanjem samo da napomenem da ukoliko nije moguće u postpunosti ispoštovati uslove slučaja uzmimo tako da bude dovoljno blizu, npr. u prvom slučaju odaberimo ):

1)
Očigledno se tangenta i prava poklapaju (pa jesu paralelne);

2,3) je središte luka (imamo dva luka pa samim tim i dva slučaja)
Ovo je zanimljivo. Tačke i odlaze u beskonačnost i zbog toga dobijamo u preseku kružnice i prave kroz paralelne sa (i time zapravo imamo ) dok je presek kružnice i prave kroz paralelne sa odnosno ! Paralelnost i sada je očigledna.

Sada da obrazložimo zašto smo ovim pokrili sve moguće slučajeve. Neka su tangente iz naših slučajeva , i odaberimo još jednu različitu od njih, . Zbog toga što je dvorazmera invarijanta važi . U ovoj jednačini nepoznata nam je samo što znači da je možemo izračunati. Kako može uzeti bilo koju vrednost time smo jednoznačno definisali jednu projektivnu transformaciju. Pokazali smo da proizvoljne tri početne vrednosti i njihove tri slike jednoznačno definišu projektivnu transformaciju. Posmatrajmo sada drugačiju transformaciju koja tangentu (koja opet "šeta") preslikava u pravu kroz njoj paralelnu. Primetimo da naše odabrane vrednosti u ovoj novoj transformaciji daju slike isto kao i transformacija što znači da se ova transformacija i transformacija međusobno podudaraju, i to bi trebao da bude kraj zadatka. Možda je još potrebno napomenuti celu ovu priču možemo ispričati za ma koju poziciju tačaka i , čime je zadatak zaista rešen.

Nadam se da sam sad bolje objasnio moju ideju, ako nekome još uvek nešto nije jasno neka slobodno pita i potrudiću se da preciziram što je moguće više.

---

Ti, naravno, mozes da uvodis definicije kakve hoces, ali ovo se obicno ne radi ovako. Projektivna prava je apstraktni objekat, i mi mozemo zaista da koristimo bilo koji od ovih sistema koje si naveo kao projektivne prave, isto kao sto mozemo da koristimo klase n-torki brojeva ili ko zna sta drugo - ali ne mozemo sve istovremeno. Ako euklidski pramen pravih (tvoja opcija B) smatramo projektivnom pravom, onda ne mozemo istovremeno u tom istom prostoru i skup tacaka euklidske prave da smatramo proj. pravom. Ukratko, ta tvoja "definicija" je samo spisak primera modela. Ali okej, idemo dalje.

Ako u "dokazu" mislis da baratas pojmovima kao sto je "konusna kriva", moras jasnije da razgranicis sta se kod tebe odnosi na model ("konfiguraciju"), a sta na projektivni prostor, narocito ako koristis dva razlicita modela ui jednom dokazu. Idealno bi, naravno, koristio samo pojmove projektivnog prostora: rekao bi "projektivna prava" i ne bi bilo bitno kakav model koristis, ali to nije u potpunosti moguce kad se euklidski problem resava projektivnom geometrijom.

Ali da predjemo na stvar.



Ovo je najbolja ilustracija naivnosti "dokaza". Postoji dobar razlog zasto se konvergencija retko koristi u geometriji, a to je cinjenica da granicne vrednosti slika retko imaju ista svojstva kao same slike elemenata kojima teze. Cela klasicna analiza je u stvari proucavanje tih "retkih" slucajeva kada se granicne vrednosti pokazuju kao korisne. Ovako olako ih metati u geometrijsku diskusiju je neozbiljno, jer se toliko vaznih svojstava gubi kad sa niza tacaka predjes na njegovu granicnu vrednost.

Slucaj A=C slobodno mozes da zaboravis jer je, kao sto sam rekao, iskljucen postavkom zadatka. Ako to i prenebregnes, podsecam te da se trazi dokaz da je AD a ne "tangenta u A" paralelna sa CS. A u ovom slucaju prava AD i ne postoji. I ako to prenebregnes, ipak ni CS ne postoji, jer ne postoji tacka S. Tacka S ne postoji jer je odredjena pravom DR, koja ne postoji. Prava DR ne postoji jer je D=R; prava nije odredjena proizvoljnim dvema tackama, nego proizvoljnim dvema razlicitim tackama. (Eto primera svojstva koje se gubi prelaskom na limes.) Tvoja tvrdnja da se "prava" (tj. CS) poklapa s bilo cim je besmislena, jer prava CS ne postoji.

Slucaj kad je A srediste luka BC (bilo kojeg od dva) je takodje iskljucen postavkom zadatka, jer tada tacka D ne postoji - tj. nije ispunjena pretpostavka "Tangenta u A kruga K(A,B,C) sece pravu BC u tacki D" - ne sece je nigde. Sustinski je uslov korektnosti euklidske geometrije to da ne postoji "tacka u beskonacnosti", a zadatak je zadat u euklidskoj geometriji. Cak i ako tu "sitnicu" nisi primetio, trebalo je da primetis da je tad M=D, sto potpuno ponistava jednoznacnu definisanost manje-vise svega. Dakle, sva tri tvoja slucaja su besmislena.


Mozda je kruna tvog dokaza to sto si "pokazao" da vazi jedan elementarni stav projektivne geometrije koji ne uspevas ni da formulises. Naime, tri proizvoljne projektivne tacke ("pocetne vrednosti") sa svojim slikama ne odredjuju uvek jednoznacno projektivnu transformaciju. Kako sad to, kad si ti dokazao da odredjuju? Greska je u tome sto koristis dvorazmeru, koja nije uvek definisana. Sta ako se neke tacke poklapaju? Onda dvorazmera ne postoji i dokaz pada u vodu.

Ispravan stav bi glasio "Tri razlicite projektivne tacke sa svojim slikama jednoznacno odredjuju projektivnu transformaciju (ravni)." Mala razlika, ali kljucna, i to nije prvi put da je previdjas.

Ali nema veze, idemo dalje.

Iduca recenica, u istom odeljku, neposredno posle tvrdjenja koje si pokazivao, govori da uopste nisi razumeo ni smisao toga sto si pokazao: "Posmatrajmo sada drugačiju transformaciju koja tangentu tA (koja opet "šeta") preslikava u pravu kroz C njoj paralelnu." Iz narednih recenica se vidi da pod ovim podrazumevas neku transformaciju koja ima svojstvo da t1, t2 i t3 slika bas u . Pa kolega, pobogu, upravo si dokazao (uz moju korekciju) da to ne moze tako! Ako si vec odabrao t1, t2 i t3, i njihove slike, onda ne mozes da kazes "hajde da se tA (koja seta) slika u neku tamo projektivnu tacku (tj. euklidsku pravu) koju ja odaberem". Ne, tA se pod uslovima koje si dao mora slikati samo u tacno jednu, odredjenu pravu, i to ce mozda biti ona prava koja tebi odgovara, a mozda i nece. Kad bi to moglo tako, mogao bi da dokazes da bilo koja transformacija slika bilo sta u bilo sta!

I cak i da je sve to tacno, kao sto nije, tu zadatak ne da ne bi bio resen, nego bi bio tek na pola puta. "Dokazao" si sve nebitne stvari a ono glavno si ostavio kao "ocigledno".


Ja nisam nikakav strucnjak za geometriju. Znam ono sto sam zapamtio s fakulteta, i pomalo sam zardjao, u tom smislu da cesto moram da razmisljam minut-dva o stvarima koje su ocigledne ljudima koji s geometrijom imaju redovan dodir. Ali ovo sto ti radis je cista ne-logika. Ocigledno znas neku pricu o projektivnoj geometriji sa dosta detalja ali bez dobre osnove. Mozda sam preterao s rasparcavanjem i kinjenjem tvoje poruke, ali ti pokusavas da govoris sa autoritetom o necemu sto poznajes samo povrsno. To nije u redu.

Da, to i jeste spisak modela, a svrstao sam ih sve zajedno zato što sam želeo da napomenem da se jedan model može preslikati u isti takav, ali može i u neki drugi - konkretno, u našem slučaju preslikavamo model D) u model B).

Dobro, moguće da je došlo do male konfuzije sa pojmovima, ali sad ću se potruditi da izbacim pojam konusna kriva gde god sam ga koristio. Prilikom "prevoda" koji sledi ću umanjiti opštost tvrđenja ali i dalje će ostati dovoljno jako za ono što nama treba.

C) skup tačaka na datoj kružnici;
D) skup tangenti na datu kružnicu.
(više od ovoga nam ne treba)

koristeći samo povlačenje prave kroz date dve tačke, crtanje kružnice kroz date tri tačke (ili datim centrom i jednom tačkom na rubu), nalaženje preseka dve prave, prave i kružnice, ili dve kružnice.

Ovo jeste bitno, mi se sve vreme nalazimo u euklidskom prostoru, i tu samo iskorišćavamo neke elemente projektivne geometrije.

Sa ovim zaista ne mogu da se složim. Uopšte ne shvatam tvoju tvrdnju da granične vrednosti slika retko imaju svojstva kao i prave slike (štaviše, i ove godine na takmičenju za izbor SCG ekipe za matematičku olimpijadu bio je zadatak u kojem je ključna stvar da se jedna tačka "pošalje" u beskonačnost i proveri šta se onda dešava, pogledaj http://www.elitesecurity.org/poruka/821016 - zadatak 2), ali i ako pretpostavim da se ovde ne razumemo baš najbolje iz nekog razloga, tvrdim da u ovom zadatku jeste slučaj da se granične vrednosti ponašaju "kako treba", i to je sve što je bitno, opšta priča ovde ne igra veliku ulogu. Da bih razjasnio svoje tvrđenje nastavljam primerima iz zadatka.

Kao što sam pomenuo, rešavam opštiji zadatak, kada trougao može da bude bilo kakav a ne samo oštrougli. Složićeš se da ako pokažem tvrđenje za sve trouglove da onda važi i za oštrougli?

Zbog ovakvih stvari sam i pomenuo limes, pa je vreme da ga i detaljnije razjasnim. Umesto uzmi da je na jako malom rastojanju od , i da mu se sve više i više približava ali da ga nikad ne dostiže, zapišimo to u obliku . Tada važi i (kada se pojavi korak sa kojim se ne slažeš slobodno ga citiraj i obrazloži zašto misliš da to nije dobro). Dalje, i tačka , a dalje prema definiciji tačke sledi da i . Sad sledi deo koji kad bolje pogledam i nije potpuno očigledan, a to je da i tačka . No, ovo se isto može pokazati bez većih problema, ako ne gledanjem u crtež onda računom, ukoliko se ne slažeš proveri ili kaži meni pa ću da sračunam ovde. Ipak, mislim da je naše neslaganje mnogo šire od jednog limesa, tj. čini mi se da ti tvrdiš da kompletna moja metoda ne valja, pa predlažem da se prvo razjasnimo oko toga a posle ćemo peglati detalje. Uostalom, upamti da ja tvrdim da možemo uzeti koja god tri slučaja hoćemo, pa ako ovaj i jeste sporan uzmimo neki drugi umesto njega, no to ćemo posle, prvo da vidimo da li se slažemo ili ne što se tiče generalne metode. Radi kompletnosti da dovršim svoju tvrdnju. Imamo dve tačke na kružnici i od kojih je fiksna a joj se približava na beskonačno malo rastojanje, da li se onda slažeš da prava teži tangenti u ? Pošto je tangenta u i te dve prave teže da se poklope.

Tačno, ali opet ne uzimamo tačku a tačno na središtu luka već na beskonačno malom rastojanju od njega. Da vidimo šta se onda dešava: tačka je "jako daleko". Onda biramo tačku i posmatramo . Taj ugao se približava nuli (ili opruženom uglu, zavisi s koje smo strane, ali poenta je ista), iako je nikad ne dostiže, opet sve gledamo kroz limes a to opet znači da prave i teže da se poklope odnosno . Do sada ne bi trebalo da bude spora. Pošto je definisana kao presek sa kružnicom, a , direktno sledi . Dakle, dok teži sredini luka teži u i u ovom slučaju vidimo paralelnost.

Verovatno sam trebao da u prošloj poruci bolje naglasim da sve gledamo kroz limes, onda možda ne bi bilo toliko nesuglasica, ali sam smatrao da se to podrazumeva.

Tačno, ali ne vidim kako bi se među tri tačke koje sam odabrao dve mogle poklopiti. Moguće je jedino u slučaju ali ako nam je to baš neophodno onda njega ispitamo posebno. Nisam smatrao da je potrebno posebno naglasiti da su tri tangente (tačke) koje sam ja odabrao različite, jer mi se činilo da je to očigledno.

Biće da nisi razumeo šta sam pokušao da kažem tom rečenicom, a to je sledeće: kada završimo sa transformacijom koja je opisana u postavci zadatka posmatramo novu transformaciju koja tangentu preslikava u euklidsku pravu kroz njoj paralelnu. Primećujemo da za tri pomenute tangente ove dve transformacije daju iste slike, pa iz toga sledi (zbog jednoznačosti) da su to dve transformacije koje se poklapaju, iz čega sledi tvrđenje. Još jednom ukratko: imamo u celoj priči dve transformacije:
1) - transformacija koja sadrži sve manipulacije opisane u postavci zadatka;
2) (nisam je nikako eksplicitno nazvao u prošloj poruci ali sad moram radi pojašnjenja) - transformacija koja tangentu slika u pravu kroz njoj paralelnu.
Sada primetimo da za odabrane ove dve transformacije daju iste slike, a to onda znači . Ovo bi trebalo da nije sporno, pogotovo što na osnovu ranijeg teksta vidim da donekle shvataš na šta mislim. E sad, to znači da za svaku vrednost važi . Pošto zapravo predstavlja pravu kroz paralelnu sa onda je i prava paralelna sa , a to je ono što treba pokazati u zadatku.

Ne znam na šta tačno misliš da je glavno što sam ostavio kao očigledno, pa te molim da malo bolje razjasniš šta si mislio.

Stoji da imam manji problem sa izrazima jer sam jako malo stvari vezanih za ovu temu čitao na srspkom jeziku tako da ne uspevam uvek da nađem adekvatan prevod. Međutim, to i dalje ne bi trebalo da predstavlja nerešiv problem jer možemo da se dovijamo raznim izrazima, bitan je postupak rešavanja. Nisi preterao sa rasparčavanjem i kinjenjem moje poruke, naprotiv, više volim kada neko sistematično, deo po deo, ukaže na ono sa čim se ne slaže (kao što si ti uradio) nego kad neko kaže: "Ma to ne valja" i završi priču. Tačno je da ima grana matematike koje poznajem daleko bolje od projektivne geometrije, ali ovde nam trebaju samo osnove, i to samo onaj deo koji se može primeniti u euklidskoj, skoro cela projektivna geometrija ostaje ispred nas i ni ne dotičemo je. Mogu pogrešiti u nekom detalju tokom rešavanja zadatka, ali zar zaista misliš da bih i počinjao na ovaj način ako znam da ne može tako? Osim toga, radi malo sređenijeg nastavka diskusije bih ti postavio jedno pitanje da imamo neku startnu tačku. Reci mi, da li smatraš da se zadatak uopšte ne može rešiti svođenjem na tri slučaja, ili misliš da je ovaj sistem u redu samo treba pogodnije odabrati tangente (da slučajevi ne budu degenerisani i granični već konkretni)?

Ne bih voleo da se ova diskusija prekine i raspoložen sam za nastavak, verujem da ćemo se na kraju ipak složiti.

---

Pre svega, vazna ispravka: mislim da sam pogresio kod price o jedinstvenosti projektivne transformacije. Naime, uslov je jos ostriji: tri tacke o kojima se govori moraju da budu nekolinearne. Ozbiljna greska s moje strane - kao sto rekoh, zardjao sam.


Ali hajdmo nazad na glavnu temu. Mislim da ne zelimo ni ti ni ja da se rasplinjujemo previse, pa zato hajde da pricamo samo o kljucnim stvarima. Kako se meni cini ovde su dva stvarno kljucna neslaganja:
1. Tvoja geometrijska upotreba konvergencije. Nju nisi spominjao bas od pocetka i nije toliko kljucna za sam dokaz - u smislu da kad bi ostatak dokaza bio ispravan, ovaj deo bi mogao da se preradi tako da stoji bez konvergencije (ali opet ne na onaj nacin kako si ti prvo bio krenuo bez nje). Ali ta neispravna upotreba je ilustracija naivnog i nedoslednog pristupa resavanju ovog problema, pa je zato ipak racunam kao kljucnu
2. Drugo nase kljucno neslaganje je o opstim pravilnostima projektivne geometrije. Ne znam kako da ga rezimiram, pa cu morati da ga samo izlozim dole.

Oko svega ostalog bismo se sasvim verovatno na kraju slozili, ali oko ove dve stvari tesko.

1. Konvergencija


U zadacima iz geometrije. Rec retko koristim uslovno i opisno, objasnicu nize. U zadacima iz analize uopste nije tako. Pogledao sam zadatak na koji linkujes (cestitam na takmicarskom uspehu!) i on nije geometrijski, a i da jeste, koliko vidim resio si ga bez limesa. (Mozda ne citam dobro - kazes zadatak 2, to je onaj sa tri broja kojima je proizvod jednak 1?)

"Prelazak na limes" je operacija koja se cesto izvodi naizgled nonsalantno i olako, ali iza nje uvek postoji neka podrazumevana, poznata i ranije dokazana teorema koja garantuje da se to sme uraditi. Izuzetak su jedino neformalne ilustracije nekih pravilnosti, od kojih se i ne ocekuje doslednost koja odlikuje prave dokaze. Kada bi se uvek moglo "preci na limes", limesi ne bi ni bili potrebni. Oni su dragoceni bas zato sto ponekad omogucavaju ono sto se bez njih ne moze.

Mogao bih da kazem "hajde ti lepo dokazi da tu smes da predjes na limes" i to bi bilo logicki korektno s moje strane, ali mozda ne bi bilo fer u ovoj situaciji - zato cu umesto toga da ti ponudim par kontraprimera koji pokazuju da se limesi ne mogu koristiti u geometriji na taj nacin:

- Neka su prave x i y paralelne i razlicite, a proizvoljna prava p sece x u nekoj datoj tacki. Ako uzmemo da ugao px tezi nuli, tada i ugao py tezi nuli. Ali mozemo li da "predjemo na limes"? Ako je ugao px jednak nuli, da li je i ugao py jednak nuli? Nije, zato sto u tom slucaju ugao py ne postoji.
- Neka su X i Y tacke na datom krugu, X fiksirana a Y pokretna. Ako Y tezi ka X, tada prava XY tezi ka tangenti tX. Ali ako je Y=X, da li je tada XY=tX? Nije, jer tada ne postoji prava XY.
- Ne mora nesto da postane nedefinisano da bi poremetilo prelazak na limes. Recimo, neka je t tangenta kruga paralelna precniku AB, a C tacka na krugu. Kad C tezi ka B, prava AC "tezi" ka pravoj t. Ali kad C postane jednako B, prava AC i dalje postoji ali nije jednaka pravoj t. (Ovo je najpre zbog ogranicenosti pojma "konvergencije" niza pravih - to nije prava konvergencija.)

U geometrijskim zadacima (onima koji nisu potpuno trivijalni) jako cesto resenja zavise od granicnih, singularnih slucajeva, koji pod limesima uvek zahtevaju dodatnu analizu. Cak se cesto upravo trazi, kao u ovom zadatku, da se dokaze da je neki dati slucaj upravo singularan. Delovi problema koji ne zavise od singularnosti se mogu bez straha resavati limesima, ali to su po pravilu oni najlaksi delovi za koje ti limesi i ne trebaju. Svojstva geometrijskih objekata koja su od najveceg interesa su diskretna, i preslikavanja samih objekata u ta njihova svojstva ne mogu biti neprekidna. Cesto su skoro svuda neprekidna, sto moze da zavede coveka, ali bas te tacke prekida su ono sto biva zanimljivo u datom problemu.



Da, s tim cu se sloziti. Ali moja primedba na koju si odgovarao se nije vise odnosila na ostrouglost trougla, nego na dublje stvari. (Moja greska, spomenuo sam to na nekom drugom mestu u poruci, ali tu sam samo sturo rekao da je taj slucaj iskljucen.) Naime, postavka zadatka podrazumeva da je trougao takav da se mogu konstruisati svi elementi koji se koriste, zakljucno s pravom CS. U slucaju koji ti predlazes vise nije ni bitna ostrouglost trougla, jer se neki od tih elemenata ne mogu konstruisati. Uzalud dokazujes da je nepostojeca prava paralelna necemu. Ovo samo objasnjavam sta sam tada imao na umu, ali sada, sa tvojim revidiranim dokazom, ta moja primedba vise ne stoji. Na zalost, stoje neke druge.



Zaista si u pravu kad kazes da kad A tezi ka C, tad i S tezi ka C. Da prave AD i CS "teze da se poklope" je pipava tvrdnja: nizovi pravih ne mogu zaista da konvergiraju, to mogu samo pramenovi pravih (ako i oni uopste mogu, nisam sasvim siguran). Ali zazmurimo na jedno oko - cinjenica je da te prave rade nesto sto lici na konvergenciju, pa hajde da se pravimo da je to prava konvergencija. Cak ni tad ovo nije "slucaj". Nisi pokazao da postoji neki slucaj kad su zaista paralelne, a to ti je bila prvobitna namera. Imas nizove pravih, koje su (kako stvari za sada izgledaju iz dokaza) neparalelne u parovima. Sto se dalje ide kroz nizove to su one, izgleda, "sve manje neparalelne", ali nisi dokazao da ce se nekad, za neki slucaj, desiti da zaista postanu paralelne.

Slicno i za slucajeve kad A postavljas blizu sredista luka BC. Nesto ili jeste paralelno ili nije, to je diskretno svojstvo. "Teznja" ka necemu je samo lep nacin da se govori o nizovima, ali na kraju mora konkretna prava da bude paralelna s konkretnom pravom.

Jesi li u pravu kad kazes da se u opstem slucaju konvergencija moze ovako koristiti? Nisi. Pogledaj egzaktne kontraprimere gore.

Jesi li u pravu kad kazes da se u ovom zadatku ipak konvergencija ponasa ispravno? Nisi. Sustinska, konkretna svojstva se gube. Pod limesom se gubi definisanost elemenata koji se zahtevaju jos u postavci zadatka, a pre limesa ti prave "nisu" paralelne (tj. nisi dokazao da jesu).

Jesi li u pravu kad kazes da se nekako mogu konstruisati primeri u kojima prave CS i AD jesu paralelne? Jesi. Zaista mogu. Samo ti to nisi uradio.


2. Projektivna geometrija

Te stvari ne funkcionisu na taj nacin.

Projektivne transformacije cuvaju incidenciju, dvorazmeru, harmonijsku spregnutost, razdvojenost parova i neprekidnost. Ne cuvaju (u opstem slucaju) raspored, meru, razmeru, podudarnost, ugaonu meru ni paralelnost. U projektivnoj geometriji ne vaze aksiome rasporeda, podudarnosti i paralelnosti. Ne postoji pojam paralelnih pravih. Ne postoji pojam sredista duzi (ni luka), jer se srediste ne moze definisati bez podudarnosti. Ne postoji pojam kruga, jer se i on definise podudarnoscu. Ne postoji pojam duzi, jer se duz definise rasporedom.

Jesi li primetio da se proizvoljan trougao* moze projektivno preslikati u proizvoljan drugi trougao? To znaci da svako projektivno svojstvo koje vazi za jedan trougao vazi za sve! Ali svojstva koja ukljucuju, recimo, paralelnost ili srediste neke duzi nisu projektivna; dve paralelne prave se mogu preslikati u dve prave koje se seku, ili se srediste duzi moze preslikati u tacku na dve trecine duzi, ili cak van duzi (ali na istoj pravoj). Opisani krug se moze preslikati u neku hiperbolu. Unutrasnji ugao trougla se moze preslikati u spoljasnji (naspramni, ne nalegli).

(* - Da ne bude zabune, govorim o nedegenerisanim trouglovima. Odgovarajuce stvari vaze i za degenerisane, samo se duze pisu.)



To je vrlo verovatno. Hajde da ja razjasnim sta sam mislio da si rekao, pa da uporedno analiziram ovaj deo tvog dokaza pod tom pretpostavkom, i pod razjasnjenjem koje si sad dao. Ovo je verovatno najvazniji deo u onome o cemu se ne slazemo.

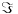
U jednoj poruci si napisao da preslikava konfiguraciju D u B, a u kasnijoj si rekao nam trebaju konfiguracije C i D, a ne B. Cini mi se da je ovo drugo bio lapsus, a da si ono prvo stvarno mislio, ali cak nije ni vazno, jer primedba koju stavljam ima veze s opstom prirodom projektivnih transformacija, a ne sa konkretnom konstrukcijom.

Zamislimo da si uspesno konstruisao tri konkretna slucaja u kojima si dokazao da vazi da je AD paralelno s CS. Zamislimo da su ova tri slucaja onoliko nezavisni jedan od drugog koliko god mogu biti (da bismo eliminisali moguce primedbe o odredjenosti transformacija, a da ne bih ja sad izmisljao pola sata kako se ta nezavisnost tacno formulise). Neka je t1 prava koja je u prvom slucaju AD, a s1 prava koja je u prvom slucaju CS. Slicno tome, neka su t2, s2, t3, s3 prave iz drugog i treceg slucaja. Neka je t4 prava koja je u proizvoljnom, neproucenom cetvrtom slucaju prava AD, a s4 prava koja u tom istom slucaju prolazi kroz C i paralelna je sa t4. Ne zameri sto menjam oznake, t4 je ono sto si ti oblezio kao tA, a meni je ovako lakse.

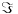
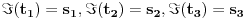
Ja sam mislio, i s ovim tvojim novim objasnjenjm i dalje mislim da si ti prvo rekao "Neka je projektivna transformacija takva da je . Znamo da ona postoji i da je jedinstvena na osnovu malocas dokazane teoreme." Okej.

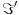
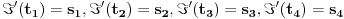
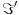
E, sad. Mislio sam da si posle toga rekao "Neka je projektivna transformacija takva da je ." Ovo sam zakljucio na osnovu nastavka tvog teksta. Ali, sudeci po tvom skorijem objasnjenju, mogu samo da zakljucim da si u stvari rekao "Neka je projektivna transformacija takva da je ."

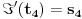
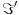
U prvom slucaju, po onome sto sam mislio da si rekao, moja primedba glasi: Otkud znas da transformacija postoji? Stavise, vrlo nedavno si dokazao teoremu koja kaze da u opstem slucaju ona ne postoji. Ako mislis da ovaj zadatak cini singularni slucaj u kojem ona ipak postoji, onda to moras da dokazes.

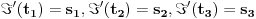
U drugom slucaju, po novom objasnjenju, primedba glasi: Otkud znas da vazi ? Pozivas se na to u dokazu, ali to ne sledi iz konstrukcije .

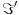
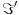
Da li je moguce da sam ponovo lose razumeo kako konstruises ? Kako god da je konstruises, neka primedba od ove vrste ce stajati, jer projektivna ravan nije dovoljno "bogat" prostor da napravis konstrukciju koju ovde zelis.

Ovo je sustinska stvar. Primedbe idu dalje, ali ovo gore je centar svega.

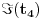
Gde idu dalje? Recimo da ta transformacija ipak postoji. Sad bi bio na pola zadatka. Nastavak tvog dokaza se oslanja na predstavu da je prava koja je konstruisana kao CS u tom cetvrtom proizvoljnom slucaju. Ovo bi vazilo kad bi konstrukcija prave CS bila cisto projektivna, ali ona to nije, jer koristi svojstva podudarnosti i rasporeda, koja se u opstem slucaju gube projektivnim transformacijama.



Verujem da si iskreno bio ubedjen da se moze resiti ovako. Ali to ubedjenje je pogresno.



Pogodniji izbor tangenti eliminise sve moje primedbe na tvoju upotrebu konvergencije, ali ne resava zadatak.

Zadatak se ne moze resiti svodjenjem na tri slucaja i primenom projektivnih transformacija. Ovo znam pre svega intuitivno, zato sto u projektivnoj geometriji "postoji" samo jedan slucaj nedegenerisanog trougla, tako da bi bilo sta sto se moze resiti sa tri slucaja moglo da se resi i sa jednim - sto nije dokaz, nego samo putokaz za intuiciju koji bi teoretski mogao da bude pogresan. Ali srecom to znam i egzaktno, zato sto svojstva koja se traze ne ostaju ocuvana kroz projektivne transformacije, i tu je kraj svake price. Problem nije projektivne prirode.

Sta je, medjutim, meni ovde zanimljivo? Da li si u pravu kad mislis da se neki projektivni problem u ravni moze resiti analiziranjem tri "dovoljno nezavisna" slucaja? Ne znam. Morao bih da znam, ali ne znam. Kopka me. Nacin na koji si ti to pokusao da uradis je neispravan, ali mi opet ta intuicija kaze da tu ima necega. Mozda se problem zasnovan na cetiri proizvoljne tacke ili druga cetiri proizvoljna elementa ("dokazati da tad vazi to-i-to projektivno svojstvo") moze resiti tako sto se nadju tri slucaja koji su nezavisni, u tom smislu da se ne mogu projektivno preslikati jedan u drugi, i onda vazi za sve cetvorke tacaka? U to bi me neko mogao ubediti, mada bih naravno radije video dokaz nego ubedjivanje.

Kada sam napisao smatrao sam da samo što to izgleda nisam dovoljno naglasio. Znači, nigde nisam ni kretao bez konvergencije, već samo nisam koristio oznake za nju već sam ih prećutno podrazumevao (jer, kao što i sam shvataš, u strogom slučaju bez konvergencije problem postaje besmislen). Ali predlažem sledeće: da za sada ostavimo konvergenciju po strani, i zamislimo da jesam pronašao, kako si sam rekao, "tri slučaja nezavisna jedan od drugog koliko god mogu biti" bez konvergencije i ostalih spornih detalja, pri kojima je zaista paralelno sa . Čini mi se da se slažeš da se mogu naći takvi slučajevi i adekvatni dokazi za njih (sa manje ili više posla). Naravno, ne pokušavam da pobegnem od objašnjavanja svoje ideje, već da napravim neki red time što ćemo se prvo dogovoriti da li je uopšte moguće ili ne raditi na osnovu ta tri slučaja, a kada se složimo po tom pitanju vratićemo se na limes. Još jedan razlog što za sada neću više pominjati limes je taj što nisi pronašao dobar zadatak na koji sam te uputio, u toj temi postoji dva zadatka koji su obeleženi brojem 2) (znam da je malo konfuzno) i mislio sam na onaj drugi - nalazi se par poruka ispod onog koji si čitao, i počinje sa: "U ravni je dat konveksni ugao..." Rešenja nema na pomenutoj temi, ali se radi tako što se najpre tačka pošalje u beskonačnost i analizira taj slučaj (tj. je "skoro paralelno" sa ), zatim se isto uradi sa tačkom i onda se gleda presek ta dva slučaja. Ovo je zvanično rešenje naše Savezne komisije pa kad se vratimo na temu limesa u geometriji valja uzeti i taj primer u obzir (a ne razlikuje se mnogo od našeg zadatka) jer ne verujem da bi neko sebi dopustio da daje na tako visokom takmičarskom nivou zadatak čije rešenje je neupotrebljivo. Na tvoje kontraprimere takođe imam šta da dodam ali na sve to ću se vratiti kasnije, zaista ne pokušavam da to ostane "zaboravljeno" već samo da se organizujemo na neki način.

Kao što rekoh, predlažem da se prvo dogovorimo oko ovog. Sledi nastavak.

Da, lapsus.

Dobro, ali kako projektivna geometrija šta definiše je za nas ovde nebitno. Sve naša transformacija se sastoji iz kompozicije sledećih preslikavanja:
1) povlačenja prave kroz date dve tačke;
2) opisivanja kružnice sa datim centrom i jednom tačkom na rubu;
3) nalaženje preseka dve prave ili prave i kružnice ili dve kružnice.
Sve ovo jesu projektivne transformacije (ili se sa tim ne slažeš?). Diskusija može da nastane oko središta, ali da bismo našli središte duži opišimo kružnice sa centrom koja sadrži odnosno sa centrom koja sadrži (2), zatim nađimo njihove preseke tačke i (3), zatim povucimo pravu (1) i na kraju nađimo presek te prave i prave (3).

Jesi, ne znam da li ja toliko loše objašnjavam ili ti imaš nešto drugo na umu dok to čitaš, ali pokušaću još jednom. Prvo, zaboravi na prave , one nam prilikom konstrukcije neće trebati. Dakle, definišemo ovako:

Nadam se da nema sad ništa nejasno, rečeno jezikom: transformacija uzima pravu i vuče njoj paralelnu kroz . Ne mogu da nađem jednostavniji opis.

E sad sledi ključna stvar: za naša tri slučaja se događa (što smo utvrdili direktnom proverom). Pošto važe sve potrebne nezavisnosti (dogovorili smo se da za momenat tako pretpostavimo) iz ove jednakosti sledi da je . Sada uzmimo neko koje još nismo birali i onda važi na osnovu gornjih zaključaka da je . Ali šta je ? To je prava gde je tačka koja se dobija na način opisan u postavci zadatka. A šta je ? To je prava koja je po konstrukciji paralelna sa . Pošto se te dve prave poklapaju sledi i da je paralelno sa . Ovo je ključna stvar i smatram da je najbitnije da se složimo u vezi sa ovim a za limese ćemo posle lako, tako da te molim da pažljivo razmotriš sve što sam napisao u ovom delu i što detaljnije opišeš to što ti nije jasno. Evo i nekih konkretnih pitanja, možda će nam ona pomoći da preciznije uvtrdimo gde se tačno ne slažemo:
1) Da li transformacija čuva dvorazmeru?
2) Da li transformacija čuva dvorazmeru (pre toga da li si razumeo kako sam napravio )?
3) Da li se transformacije i poklapaju?
4) Da li iz 3) sledi rešenje zadatka?

---

Okej, znaci konvergenciju si od pocetka podrazumevao. Ako bas hoces da se posle vratimo na nju, mozemo, ali ne vidim potrebu za tim. Slazemo se barem da nije neophodna za ostatak tvog resenja. Jedino ako zelis da i dalje branis svoju ideju da se ona moze ovako koristiti.

Sto se tice zadatka na koji si hteo da linkujes, nasao sam postavku ali ne i resenje. U svakom slucaju, ne kazem da se nikad, nikad ne moze koristiti konvergencija u geometriji. Kazem da je tvoja upotreba ovde bila pogresna, a pored toga primecujem da postoji dobar razlog zasto se u praksi kortisti retko.



Bitno je sta uopste definise a sta ne. Taj deo mog teksta nije bio kritika na tvoju konstrukciju transformacije, nego ukazivanje na opsta svojstva projektivne geometrije sa kojima, moram da ponovim, lose baratas. Ti ocekujes (kasnije u dokazu) od projektivnih transformacija da ocuvaju neka svojstva koja one ne cuvaju.



Ne slazem se. Prvo, ovo su konstrukcije a ne preslikavanja. Ali razumem sta si mislio. Opisivanje kruga sa datim sredistem nije projektivna operacija nikoje vrste u ovim tvojim konfiguracijama. Pretpostavljam da termine "tacka", "prava" i "kruznica" koristis u euklidskom smislu, i u to u kontekstu konfiguracije A, jer u projektivnom smislu ne postoji pojam "kruznica" (ni "krug").

Sta je krug, kolega? Skup tacaka B takvih da je par SB podudaran paru SA, gde su S i A zadate (razlicite) tacke. Ali podudarnost ne postoji u projektivnoj ravni!

Ti insisiras na tome da konstruises krugove i sredista duzi u projektivnoj ravni. Stvarno ne zelim da zvucim nadmeno, ali kad to toliko puta ponovis sa tolikom sigurnoscu, to pokazuje nerazumevanje stvarno najosnovnijih pojmova projektivne geometrije. Vidi se, priznajem, da znas dosta njenih pojmova i pravilnosti, ali to je povrsno. Saplices se na samim osnovama.



... gde i ide od 1 do 3 ili od 1 do 4? Izgleda da imas na umu 3.

Ako i iz konstrukcije ide od 1 do 3, primedba glasi: Otkud znas da je "prava koja je po konstrukciji paralelna sa AD"? To bi (verovatno*) vazilo kad bi bila koincidencija, ili neka izometrija, ili neka transformacija slicnosti. Ali je opstija od svega toga, ona je projektivna transformacija i samo se u specijalnom slucaju moze desiti da to zaista vazi. Ako mislis da je ovaj zadatak jedan od tih specijalnih slucajeva, onda to moras da dokazes.

A ako slucajno i iz konstrukcije ide od 1 do 4, primedba opet glasi (copy/paste): Otkud znas da transformacija postoji? Stavise, vrlo nedavno si dokazao teoremu koja kaze da u opstem slucaju ona ne postoji. Ako mislis da ovaj zadatak cini singularni slucaj u kojem ona ipak postoji, onda to moras da dokazes.

(* - "Verovatno" znaci da usled zardjalosti nisam sasvim siguran u ovo, a ne da bi u "vecini" slucajeva vazilo. U drugi deo tvrdnje sam sasvim siguran.)



1) Da.
2) Da, ako sam dobro razumeo da indeks i u njenoj konstrukciji ide od 1 do 3
3) Da
4) Ne. Ako ni zbog cega drugog, onda zato sto nisi dokazao .



[izmena: popravio sam jedan mali lapsus koji sam bio napravio.]

_{[Ovu poruku je menjao Vladimir P. Filipovic dana 22.09.2005. u 16:42 GMT+1]}

Definišem transformaciju koja za svaku tačku pravi pravu kroz koja je njoj paralelna. Onda je po konstrukciji zaista paralelno sa . Sad je pitanje zašto čuva dvorazmeru. Jednostavno, uzmimo neke četiri (ovo ne moraju biti one "specijalne" koje smo do sada koristili nego ma koje četiri). Posmatrajmo preslikavanje koje ih slika, redom, u (možemo reći, na primer, polarno preslikavanje u odnosu na kružnicu koju imamo). Njihova dvorazmera ostaje nepromenjena. Zatim novom transformacijom dobijamo prave , redom, gde je centar kružnice. Dvorazmera i dalje ostaje nepromenjena jer smo samo spojili naše tačke sa konstantnom tačkom . Primetimo i to da su normalne na , redom. Dalje, rotiramo dobijene prave za ugao od oko tačke . Dvorazmera ostaje nepromenjena jer je rotacija transformacija podudarnosti. I poslednje, translirajmo prave za vektor . I time dvorazmera ostaje nepromenjena, a dobili smo upravo transformaciju .

Sad moram da kažem: u pravu si, pogrešio sam, i time sve (nažalost) pada u vodu. Ono što jeste projektivna operacija je opisivanje konusne krive kroz pet tačaka, i skroz sam bio slep da mislim da je to isto to, ne znam šta mi je bilo. Naime, ni ja ni ti se nismo mnogo zadržavali na samom ovom detalju, i svaki put sam ga preskakao misleći da je to očigledno i da nema spora.

Nisam ja sve ovo sad izmislio, već sam se poveo drugim problemima koji se mogu rešiti na sličan način. Navešću dva takva (zajedno sa rešenjima) pa možemo zajedno da ih pogledamo.

1) je prečnik kruga. i su tačke na tangenti u , sa različitih strana tačke . Prave i ponovo seku kružnicu u tačkama , redom. Prave i ponovo seku kružnicu u tačkama , redom. Pokazati .

Rešenje:
Fiksirajmo i pomerajmo . Definišimo transformaciju . Dokazaćemo da je ona projektivna. Najpre, je projektivna jer se nalazi u preseku kružnice i prave . Dalje je projektivna jer preslikava pramen pravih kroz u pramen pravih kroz tako da se original i slika seku na pravoj . Samim tim, i je projektivna. Kompozicijom dobijamo i da je projektivna, a iz toga neposredno sledi i je projektivna. Ako koristimo ranije oznake, to je naša transformacija , za koju smo upravo dokazali da čuva dvorazmeru. Transformaciju definišemo kao osnu simetrija u odnosu na pravu , a pošto je to transformacija podudarnosti očigledno i ona čuva dvorazmeru. Dakle, ukoliko pokažemo da se navedene dve transformacije poklapaju za neka tri slučaja, one se poklapaju uvek. Uzmimo sledeće slučajeve:
a) - ovaj slučaj je trivijalan jer je cela slika simetrična u odnosu na pravu ;
b) - dešava se , pa je očigledno da se transformacije poklapaju;
c) - dobro, možemo i bez limesa :) Paralelne prave se seku u beskonačnoj tački, i to za svaki pramen takvih pravih imamo jedinstvenu tačku. U ovom slučaju to je tačka . Dakle, sve što smo u postavci definisali kao sada postaje prava kroz paralelna sa (jer i sadrži pa je to taj pramen). Dakle, imamo , simetrično (u odnosu na ) i pa se i ovde i poklapaju.

U vezi sa ovim poslednjim slučajem da napomenem da isto tumačenje možemo da iskoristimo i prilikom slučajeva kada je središte luka u početnom zadatku, i time izbegnemo taj limes (mada onaj prvi i dalje ostaje).

2) Trouglovi i su jednakostranični. Prava kroz seče i u , redom. Naći ugao između i .

Rešenje:
Ako "šeta" onda je transformacija projektivna (ovog puta zaista očigledno) - neka je to . Neka je rotacija oko za ugao od - očigledno čuva dvorazmeru. Primetimo još i to da možemo definisati i kao transformaciju pri kojoj je (orijentisani uglovi), pri čemu nam je ovakva definicija pogodnija za dalji rad. Kao i u prethodnom zadatku, uzimamo sledeća tri slučaja:
a) - imamo i ;
b) - ovog puta je dok je tačka u beskonačnosti. Važi da je (to što je u beskonačnosti nam ne pravi problem jer su sve prave koje je "sadrže" međusobno paralelne, pa za računanje ugla možemo iskoristiti bilo koju od njih, npr. );
c) - ovog puta je dok je u beskonačnosti, ali ostatak priče je analogan slučaju b).

To su bili neki primeri kako se ova ideja može lepo iskoristiti, interesuje me šta misliš o njima (i da li opet ima nekih nesuglasica).

---

Drago mi je sto smo se oko ovoga slozili, ali to je manja greska od jedne druge stvari. Ako nemas nista protiv, voleo bih da nju isteramo do kraja na cistac:



(Mislis, paralelna nekoj pravoj, recimo konstruisanoj AD.) Ovo je stvar koju ne mozes ni u snu da napravis. Tj. ovakva transformacija mozda i postoji, ali nemas nikakvu garanciju da je projektivna. Cak mi se cini da nije dobro definisana, jer se za razlicite trouglove ABC (s razlicitim tackama C) moze dobiti ista prava AD.

Tvoja fundamentalna greska, nezavisno od pocetnog zadatka, lezi u ocekivanju da projektivna transformacija koja slika tri prave u njima paralelne slika svaku pravu u njoj paralelnu, i ne vidim da smo to pitanje razresili. Paralelnost je ovde puka slucajnost. Mozda (nisam siguran) se nesto slicno moze dokazati ako proj. transf. slika pet pravih (od kojih su svake tri nekonkurentne) u njima paralelne, ali tada se (cini mi se) ta projektivna transformacija uvek moze predstaviti kao translacija ili homotetija; u svakom slucaju, ovo bi bio sasvim drugaciji (i tezi) problem nego sa tri primera, jer pet originala i pet slika u opstem slucaju ne odredjuju proj. transformaciju.

Ali da ne skrecem sa teme. Jos jednom, projektivna transformacija moze da slika tri prave (ma kako dobro izabrane) u njima paralelne prave i da neku cetvrtu ipak ne slika u njoj paralelnu. Mogu i primer da konstruisem ako treba. Ovo nije neki mracni cosak te oblasti, nego najosnovnije svojstvo.

Sto se tice tih primera zadataka, rado cu ih pogledati, ali ne mogu sad (na poslu sam). Javicu se veceras ili tako nekako.

Transformacija sigurno postoji, bila projektivna ili ne - zašto ne bi postojala kada kažem: "uzmi ovu pravu i povuci njoj paralelnu kroz "? Tačno je da se može dobiti ista prava za različite trouglove, ali ne u ovim uslovima - i su fiksne, a samo se menja. E sad samo treba dokazati da ona zaista čuva dvorazmeru, a mislim da sam to pokazao u prošloj poruci. Ako se ne slažeš sa mojim dokazom tog svojstva onda bih te molio da izdvojiš deo gde sam napravio grešku.

Naravno da možeš da konstruišeš primer, ali to nije bitno. Problem je što ja ne pričam o tamo nekom konstruisanom slučaju, već o transformaciji čiji je domen isključivo skup tangenti na datu (fiksnu) kružnicu, a kodomen isključivo pramen pravih kroz datu (fiksnu) tačku. Još jednom bih zamolio da pogledaš moj dokaz da takva transformacija čuva dvorazmeru, a iz same te činjenice sledi (ili ne?) da je jedinstvena.

---

Ja bih se vratio na sam pocetak (nisam se udubljivao u ostale postove).



Da li se ovde pozivas na neku teoremu iz projektivne geometrije, ako da jel mozes precizno da je navedes.

Ovo kako si napisao nema mnogo smisla. Prvo, ako si dokazao jedan "proizvoljan" slucaj, sta ce ti ostala dva? Ako si mozda mislio na specijalne slucajeve, lako je pokazati da teorema nije tacna (npr. dokazom da je svaki trougao jednakostranican).

Mislio sam na tri slučaja koja ja odaberem kako hoću. Teorema na koju sam se pozivao glasi: ako se dve projektivne transformacija poklapaju u tri različite tačke (i ako pri tome važe još neki uslovi koji su opisani u narednim porukama), onda se poklapaju u svim tačkama. Teorema je posle i dokazana a dodatno je rečeno još mnogo toga, tako da bih predložio da ako želiš da se uključiš u diskusiju ipak prvo sve pročitaš jer nema smisla ponavljati priču još jednom.

---

Ako ne zamerite, ne bih da se ukljucujem u diskusiju.

Jedino me zanima postavka teoreme. Ako ti nije tesko da je ponovo formulises sa svim neophodnim uslovima (znam da si rekao da se nalazi u prethodnim postovima, ali zaista su predugacki...).

OK, pokušaću.

Imamo sledeća 4 modela:
A) skup tačaka na datoj pravoj;
B) skup pravih kroz datu tačku;
C) skup tačaka na datoj konusnoj krivoj;
D) skup tangenti na datu konusnu krivu.

Posmatrajmo sada transformaciju koja elemente nekog od ta četiri modela slika u elemente nekog drugog modela (može i istog takvog) i koja pri tome čuva dvorazmeru (cross-ratio). Tada je ta transformacija jednoznačno određena sa svoja tri različita originala i tri odgovarajuće slike.

Posledica: ako imamo dve transformacije za koje važe navedeni uslovi, i pri tome se te transformacije poklapaju u tri tačke onda su one identične.

Onu prvu poruku (iz koje si citirao deo) nemoj ni da gledaš - to nema veze ni sa čim, pisao sam u velikoj žurbi i zbog toga jako lupio. Kasnije sam se ispravio i napisao ono što sam zapravo hteo da kažem ali smo ustanovili da sam ipak napravio previd i da to ne može da prođe kod ovog zadatka jer prva transformacija ne čuva dvorazmeru. Takođe smo imali i manju zbrku sa terminologijom a osim toga smo se nadugačko dotakli i priče o primeni limesa u geometriji, pa otud tolika diskusija. Ako želiš da vidiš kako ovo što sam formulisao zapravo izgleda u praksi naveo sam dva korektna primera:


_{[Ovu poruku je menjao Bojan Basic dana 25.09.2005. u 00:29 GMT+1]}

---

Okej, ovo sto kazes baca novo svetlo. Cinjenica je da sam do sad pogresno razumeo kakvu to transformaciju gradis. I dalje nisi u pravu, ali sto se vise razjasnjava sta si mislio, to mi se vise cini da ipak ima nesto iza svega toga - to jest, da postoje neki problemi koji se mogu na slican nacin resiti.

(Da li sad dobro razumem: Ti fiksiras tacke B i C i onda kazes "za svaku tacku A konstruisemo odgovarajucu pravu AD i pravu njoj paralelnu kroz C. Nasa transformacija je ona koja za svaku tacku A slika 'njenu' jednu pravu u 'njenu' drugu"?)


Prvo, konkretno za dva zadatka koje si dao kao primere:

U prvom zadatku tvoji "slucajevi" b) i c) su neispravni jer eksplicitno krse uslov iz postavke "C i D su sa razlicitih strana tacke B". Osim toga, slucaj c) je neispravan i zato sto neispravno koristi beskonacnost - o ovome sam vec govorio nadugo i nasiroko. Molim te nemoj u euklidskom kontekstu da govoris stvari kao "paralelne prave se seku u beskonacnosti", u geometriji se drzi do terminologije ne zbog pedantnosti nego zbog logicke ispravnosti. Konkretno, ako obogatis euklidsku ravan tackama u beskonacnosti, gubis izmedju ostalog svojstva poretka tacaka. (Neki zadaci mogu lepo da se preformulisu tako da pokriju "beskonacne" slucajeve prividno bez izlaska iz euklidske geometrije, zamenom tacaka pramenovima. Ali ovo nije jedan od njih - cak ne zbog poretka, nego zbog podudarnosti.)

Ali recimo da ipak imas tri dobra slucaja, sto znam da je moguce konstruisati, iako ti to nisi uradio. Sta onda? Zar nisi primetio da ti u stvari dokazujes da ce se za proizvoljan izbor tacaka slikati G u H osnom simetrijom u odnosu na AB? Ovo ocigledno nije tacno - moze biti tacno samo kad su duzi BC i BD podudarne. Takvim metodom bih mogao i ja da dokazem, na primer, da su proizvoljne dve duzi podudarne.

Pa gde je onda tacno greska u dokazu? Evo gde:



(To si objasnio Predi.) Ova "teorema" nije tacna. Bice tacna kad "tri razlicite tacke" zamenis s "tri nekolinearne tacke", sto u nasem slucaju znaci "tri nekonkurentne euklidske prave". Ali gle! Prave iz primera su konkurentne. Uvek, za ma koja tri (ili vise) primera. Ovo znaci ili da uopste ne definisu projektivnu transformaciju (sto ovde ipak nije slucaj) ili da definisu celu familiju transformacija od kojih je samo jedna ona tvoja osna simetrija (sto jeste slucaj).

Slicno u drugom primeru: prave su ti konkurentne. (Osim toga sto bar jedan slucaj opet nije ispravan, i osim toga sto sad konkretna izabrana izometrija zavisi od promenljive tacke M, sto bi - cini mi se - oborilo dokaz cak i kad bi sve ostalo stajalo.)


U pocetnom zadatku, sad kad kapiram sta si mislio, stoji ista primedba. Tri kolinearne projektivne tacke sa svojim slikama ne mogu da odrede jednoznacno projektivnu transformaciju.

(Imam i dalje neke druge, sitnije primedbe na odredjenost samih prostora koje koristis, ali njih bi sigurno mogao da otklonis uz nesto prerade dokaza, tako da nema smisla da dalje smaram. Stvarno mi je trebalo da dodje neko i kaze "ako ne zamerite, ne bih da se ukljucujem u diskusiju" da shvatim koliko smo zabrazdili u formalnosti, promasujuci dva-tri puta bitnije stvari. Hvala, Predo, sto si isterao na cistac stvarnu kosku, jer ja sam se jurio kroz nekoliko predugackih poruka oko stvari kao sto je cuvanje paralelnosti ili podudarnosti kroz projektivne transformacije, za koje se na kraju ispostavilo (ako dobro kapiram) da ih Bojan jeste podrazumevao ali mu ipak dokaz nije zavisio od njih.)


Ostaje ipak utisak da tu ima nesto. Na neki slican nacin se neki zadaci mogu resiti. Dokazati da neko netrivijalno projektivno svojstvo vazi za proizvoljne cetiri tacke. Nadjes tri primera i onda nesto nekako ispetljas. Mozda. Ne mogu sad da mislim o tome

Da, baš tako :) Zapravo, imamo dve transformacije, i za koje pokušavamo da dokažemo da su jednake, slika u (gde se dobija kako je opisano u zadatku), dok samo povuče paralelnu kroz .

OK, izbaci taj uslov i dobiješ opštiji zadatak koji onda rešavam.

Hm... Hajde da uradimo ovako. Slažemo se da kad uzmemo slučaj beskonačnosti da je onda zadatak nedefinisan. Znači, zadatak treba rešiti tako da kad je neki "normalan" slučaj onda dokazujemo to što treba, a kad je neki "paralelan" slučaj onda njega ne gledamo i kažemo: "ovo nije u postavci zadatka". E sad ja kažem ovako: uzmimo i malo proširimo postavku zadatka tako da dobijemo opštiji (naravno, ako rešimo taj opštiji iz njega sledi i ovaj početni). Proširenje se sastoji u tome da kažemo ovako: ako je slučaju "nesporan" onda nema problema, dok ukoliko imamo paralelne prave koje treba da se seku onda ćemo umesto pramena pravih koje treba da prolaze kroz tu njihovu zajedničku tačku uvesti pramen paralelnih pravih. Zapravo, čini mi se da i ti sam ovo spominješ u naredne dve rečenice, ali onda si odjednom rekao da to ne možemo da učinimo u ovom zadatku bez obrazloženja. Zašto? Da li se to što sam uveo kosi sa nekim uslovom u zadatku? Koliko vidim, zadatak je u tom slučaju bio nedefinisan a ja sam ga definisao i tako proširio, ne kvareći ono što se tražilo bez tog slučaja.

Primetio sam, i to i hoću da dokažem.

Apsolutno se ne slažem, pročitaj još jednom i videćeš da je to zapravo ekvivalentno tvrđenju zadatka. Zapravo, pokušaj da nađeš samo jedan primer kada to nije tačno i videćeš da nećeš uspeti.

Ne vidim tačno kako, ali pokušaj pa onda možemo diskutovati o tome.

Ovo sad moramo isterati na čistac jer se zaista žestoko ne razumemo. Znam da se dvorazmera može definisati i za nekolinearne (nekonkuretne, štagod...) tačke, ali to baš nigde ne koristimo, već samo ovaj specijalan slučaj. Nije nikakvo čudo što su naše prave iz primera konkurentne kada ih tako moram uzeti da bih primenio teoremu - tome prethodi cela ona priča o "modelima" ili kako smo ih već nazivali. Što se tiče same teoreme, ako se ja dobro sećam (a i ako se ne sećam mogu da skrolujem nekoliko poruka gore) ja sam nju dokazao i, što je još zanimljivije, ti si se složio sa mojim dokazom, jedino si imao primedbu na to što nisam naglasio različitost. Onda si posle rekao da moraju da budu nekolinearne ali sam prešao preko toga misleći da se radi o lapsusu i da si želeo da kažeš kolinearne pa nisam želeo da produžujem ionako dugačku poruku zbog obične greške u kucanju, kako sam bio ubeđen. No, sada to ponavljaš i ja te moram zamoliti da nađeš grešku u mom dokazu teoreme i ukažeš na nju, pošto ne vidim drugi način da ovo raspravimo a to je zapravo ključ svega o čemu pričamo.

Pravu naravno jesu konkurentne jer preslikavamo pramen pravih kroz u pramen pravih kroz . Tačka jeste promenljiva, ali možda si prevideo činjenicu da je sve ostalo fiksno (osim naravno tačke ).

Jasno bi mi bilo da si ovo tvrdio na početku priče, ali nakon što sam izneo dokaz, ti ga pročitao i (još jednom napominjem) složio se sa njim sad odjednom bez konkretnih argumenata tvrdiš da to nije tačno. Nisam uvek u pravu ali kad pogrešim volim da mi neko konkretno ukaže na grešku pa te još jednom molim da pročitaš moj dokaz i ukažeš na deo sa kojim se ne slažeš. Da ne bi morao da prelistavaš sve ove poruke (a usput da može i gpreda da se priključi i da mišljenje bez čitanja celog ovog romana) navešću dokaz ponovo.

Neka projektivna transformacija slika (kolinearne) različite tačke u (kolinearne) različite , redom. Posmatrajmo sada tačku kolinearnu sa i različitu od njih. Interesuje nas koje su sve moguće vrednosti za . Pošto transformacija čuva dvorazmeru, važi da je , odnosno ( označava usmereno rastojanje između tačaka i , tj. može biti pozitivno ili negativno).

Odavde lako nalazimo

Pošto su sve veličine na desnoj strani različite od nule, sledi da je desna strana neki realan broj, nazovimo ga . Poznato je da pravoj možemo naći tačno jednu tačku takvu da je (napominjem da sad dolazi do izražaja orijentisana dužina, u suprotnom bi postojale tačno dve takve tačke), ako je potrebno mogu i ovo da dokažem ali smatram da se radi o dovoljno poznatoj činjenici, no ako ipak insistiraš na dokazu kaži. Sledi da postoji jednistvena .

Nema potrebe da mnogo misliš, naveo sam primere za koje znam da su tačni, treba samo da mi objasniš šta ti nije jasno u dokazu teoreme a kada se oko toga složimo navedeni primeri slede kao posledica.

---

Tri kolinearne projektivne tacke sa svojim slikama ne mogu da odrede jednoznacno projektivnu transformaciju ravni.

Evo ga prost primer: uzmimo koincidenciju i osnu simetriju u odnosu na pravu s. To su dve razlicite transformacije koje imaju iste slike za pravu s.

Bojane, ti si dokazao da tri kolinearne projektivne tacke sa svojim slikama jednoznacno odredjuju projektivnu transformaciju prave, ali to ne vazi i za ravan.

U pravu si, ali gde sam ja spominjao ravan? Pričam o projektivnoj transformaciji koja ima fiksan domen i fiksan kodomen (recimo, u prvom zadatku i domen i kodomen je pramen pravih kroz tačku , a u drugom domen je pramen pravih kroz tačku a kodomen pramen pravih kroz tačku ). I kad sam formulisao teoremu pomenuo sam ona četiri "modela" i posebno naglasio da elemente jednog modela slika u elemente nekog drugog modela (eventualno istog takvog), nigde nisam pominjao šta se dešava sa originalima koji ne pripadaju domenu. Kako izgleda transformacija za ostatak ravni me uopšte ne interesuje, dokazao sam ovaj slučaj koji mi treba i na osnovu njega rešavam zadatak.

---