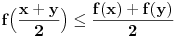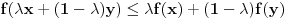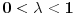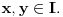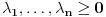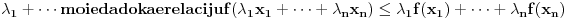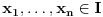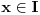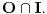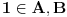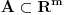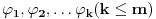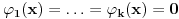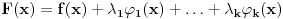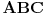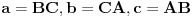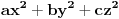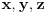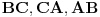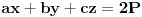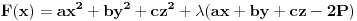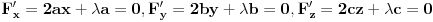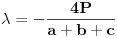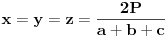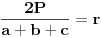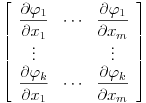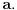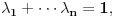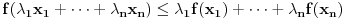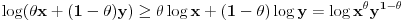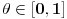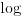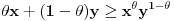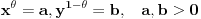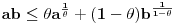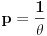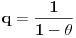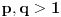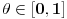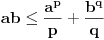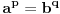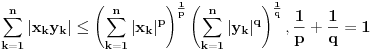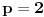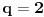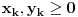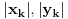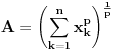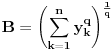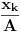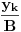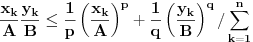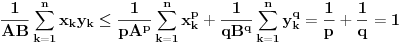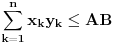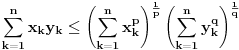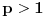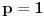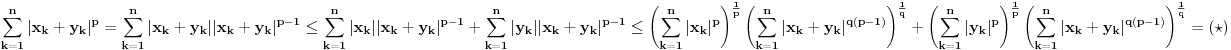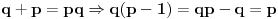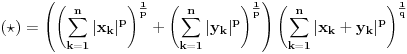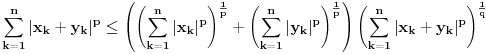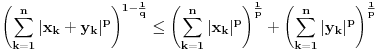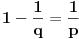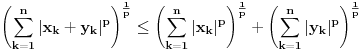 Za proizvoljne realne brojeve
Za proizvoljne realne brojeve 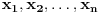 vazi:
vazi: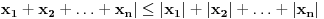
 Za
Za 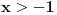 i
i 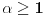 vazi
vazi 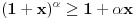 .
. Za realne brojeve
Za realne brojeve  i
i 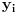 ,
, 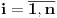 vazi:
vazi: 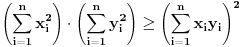
Jednakost vazi akko
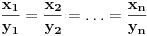 .
. Ako za pozitivne brojeve
Ako za pozitivne brojeve  i
i  vazi
vazi 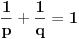 , tada za svaki par
, tada za svaki par -torki realnih brojeva
-torki realnih brojeva  i
i 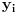 vazi:
vazi: 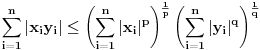
Jednakost vazi akko
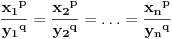 .
.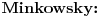 Neka je
Neka je 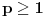 i
i 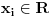 i
i 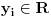 za
za 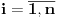 . Tada vazi:
. Tada vazi: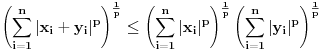
Jednakost vazi akko
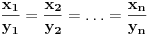 .
. Ako je funkcija
Ako je funkcija 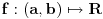 konveksna i
konveksna i 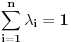 ,
, 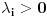 i
i 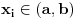 tada vazi:
tada vazi: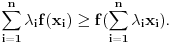
Funkcija
 je konveksna na intervalu
je konveksna na intervalu 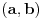 ako za svako par brojeva
ako za svako par brojeva 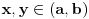 vazi
vazi 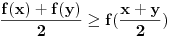 , sto je ekvivalentno sa uslovom
, sto je ekvivalentno sa uslovom 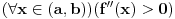 . Ako je funkcija
. Ako je funkcija  strogo konveksna, tada jednakost vazi akko su svi
strogo konveksna, tada jednakost vazi akko su svi  medjusobno jednaki ili su svi
medjusobno jednaki ili su svi 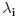 sem jednog jednaki
sem jednog jednaki  .
. Ukoliko realni brojevi
Ukoliko realni brojevi 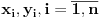 zadovoljavaju uslov:
zadovoljavaju uslov: 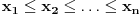 i
i 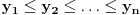 tada vazi:
tada vazi: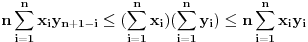
Jednakost vazi akko
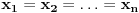 ili
ili 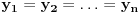 .
.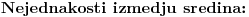 Neka je za
Neka je za 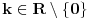 , sredina
, sredina  -tog reda:
-tog reda: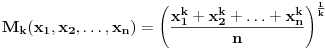
 rastuca funkcija po
rastuca funkcija po  , odnosno
, odnosno 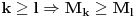 . Specijalno
. Specijalno 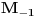 je harmonijska,
je harmonijska, 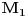 je aritmeticka,
je aritmeticka, 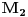 kvadratna, a
kvadratna, a 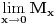 geometrijska sredina brojeva
geometrijska sredina brojeva 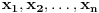 . Zbog toga vazi nejednakost medju sredinama
. Zbog toga vazi nejednakost medju sredinama 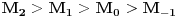 .
.Jednakost vazi akko
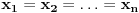 .
. Za pozitivne brojeve
Za pozitivne brojeve 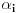 za koje va\v zi
za koje va\v zi 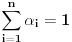 , nejednakost izmedju aritmeticke i geometrijske sredine glasi:
, nejednakost izmedju aritmeticke i geometrijske sredine glasi: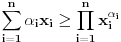
Jednakost vazi akko su svi
 medjusobno jednaki ili su svi
medjusobno jednaki ili su svi 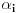 sem jednog jednaki
sem jednog jednaki  .
.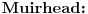 Za niz realnih brojeva
Za niz realnih brojeva 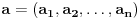 Definise se funkcija
Definise se funkcija  sa
sa  promenljivih:
promenljivih: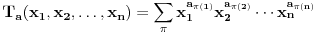
gde se sumiranje vrsi po svim permutacijama
 skupa
skupa 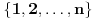 . Ukoliko za dva niza realnih brojeva
. Ukoliko za dva niza realnih brojeva  i
i  vazi:
vazi: 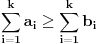 za
za 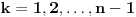 i
i 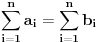 , tada vazi za sve
, tada vazi za sve  -torke nenegativnih brojeva i nejednakost:
-torke nenegativnih brojeva i nejednakost: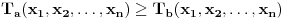
Jednakost vazi akko su
 i
i  identicni ili kada je
identicni ili kada je 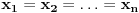 .
. Za nenegativne realne brojeve
Za nenegativne realne brojeve  ,
, 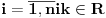 vazi:
vazi: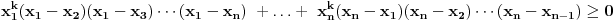
Jednakost vazi akko je
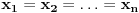 .
. Niz
Niz 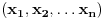 majorira niz
majorira niz 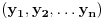 ako vazi
ako vazi 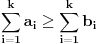 za
za 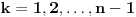 i
i 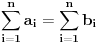 . To je neophodan i dovoljan uslov da za svaku konveksnu funkciju vazi:
. To je neophodan i dovoljan uslov da za svaku konveksnu funkciju vazi: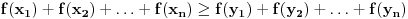
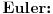 Za nizove realnih brojeva
Za nizove realnih brojeva 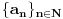 i
i 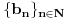 definisane sa
definisane sa 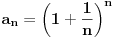 i
i 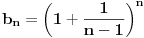 vazi:
vazi:




 [Teoreme] Nejednakosti
[Teoreme] Nejednakosti