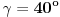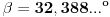Citat:
jans: A onda, pošto ne koristimo trigonometriju i inverzne trigonometrijske funkcije, treba odrediti, pomoću numeričke analize, koji to ugao u nekom pravouglom trouglu ima isti karakterističan količnik kao nepoznati ugao, ili proveriti u unapred pripremljenim tablicama karakterističnih količnika oštrih uglova.
Pročitaj pažljivo
ovu moju poruku.
Citat:
jans: Međutim, ne vidim svrhu ovakvog postupka koji je i duži i složeniji od postupka sa trigonometrijom. Naravno, možemo i tako rešavati zadatak, ali opet je to kamuflirana trigonometrija.
Upravo je u tome suština. Definicije ne smeju biti kreativne, što znači sledeće:
1. Svaki iskaz u kome se koristi definisani pojam je ekvivalentan nekom iskazu u kome se ne koristi definisani pojam, s tim da se dokay ekvivalencije iyvodim korišćenjem definicije.
2. Za svaki iskaz u kome se ne koristi definisani pojam koji je dokaziv korišćenjem definisanog pojma važi da je dokaziv i bez definisanog pojma.
Ne sme definicija da proizvodi zaključke u kojima se definisani pojam ne pojavljuje, a do kojih se nije moglo doći bez definisanog pojma. Definisije služe samo da skrate i pojednostave stvari, a ne da proizvedu nešto suštinski novo što bez njih nije bilo moguće. Naravno da su vrlo korisne.
To važi i za definicije trigonometrijskih funkcija.
Citat:
jans: Naravno, možemo i tako rešavati zadatak, ali opet je to kamuflirana trigonometrija.
To je rešenje dobijeno od drugog rešenja postupkom eliminacije definicija.
Citat:
jans: Još jednom napominjem da sam, kada sam u navedenim temama napisao da mi nije poznato da li je moguće zadatke u tim temama rešiti Euklidskom geometrijom, mislio na geometriju koju smo učili u srednjoj školi, geometriju bez trigonometrije (i bez kamuflirane trigonometrije i analitičke geometrije), odnosno rešiti elementarno.
Eliminacijom definisanih pojmova dobijaš rešenje koje ne koristi te pojmove. Možeš to nayivati kamuflažom, ali je činjenica da definicije trigonometrijskih funkcija nisu kreativne. U suprotnom ne bi bile korektne.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.




 Geometrijski zadaci i trigonometrija
Geometrijski zadaci i trigonometrija