@osvetakana, prepoznaješ li ove formule:
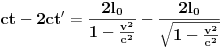
i

?! Koliko "sistema" vidiš?!
Već sam ti dao "komentar" (23 poruke prije), a, također, sam ti napisao da
sve izvodim počev od zakona puta:
PC = ct i PB = vt
@Nedeljko, prethodnu Ajnštajnovu formulu sam ti plasirao zbog tvog izmišljanja "baba i žaba" ( a ne zbog energija, mada bi i to moglo doći na red otprilike za sljedećih sedam godina zamajavanja sa tobom).
Sada ponovo tvrdiš za x i x' da su "babe i žabe" (čime potvrđuješ i svoje matematičko neznanje), čak i u Lorencovim ("boost") formulama za transformaciju koordinata:


.
Pa još "babu" - x i "žabu" - x' posmatraju u istim fizičkim zbivanjima, pa ih i međusobno dovode u nekavu vezu i međuzavisnost, pa još su i dužine duži, pa još im i zajednički "gama faktor" ( u konkretnim primjerima i iste brojne vrijednosti , za zadano n = c/v).
Ovo što si napisao treba trajno sačuvati kao primjer razmišljanja jednog dobrog matematičara i njegovom "poznavanju" Specijalne teorije relativnosti A. Ajnštajna:
Code:
x i t su nezavisno promenljive jednog sistema, a x' i x su promenljive dva sistema. Dakle, babe i žabe.
Blamiraš se, Nedeljko!
Citiram tekst A. Ajnštajna: „Da smo umjesto zakona širenja svjetlosti bili uzeli za osnovu prešutnu pretpostavku stare mehanike o apsolutnom karakteru vremena i dužina, tada bismo ujesto ovih jednadžbi transformacije došli do jednadžbi
x' = x – vt , y' = y , z' = z , t' = t
Koje se često nazivaju i „Galilejeve transformacije“. Galilejeve transformacije proizilaze iz Lorentzovih jednostavno tako da u ove potonje za brzinu svjetlosti c stavimo beskonačnu vrijednost.
Na slijedećem primjeru ćemo lijepo vidjeti kako je shodno Lorentzovim transformacijama zakon širenja svjetlosti u vakuumu sačuvan i za referentno tijelo K i za referentno tijelo K'.
Pošaljimo duž pozitivnog kraka x-osi svjetlosni signal te neka on putuje shodno jednadžbi
x = ct ,
dakle brzinom c. Shodno jednadžbama Lorentzovih transformacija taj jednostavan odnos između x i t uvjetuje i odnos između x' i t'. Ustvari, daju nam prva i četvrta jednadžba Lorentzovih transformacija kad u njih umjesto x stavimo ct:

i

. Iz kojih zatim dijelenjem dobivamo jednostavno
x' = ct' .
Prema toj jednadžbi vlada se širenje svjetlosti ako ga promatramo u odnosu na K'. Vidi se dakle da je brzina širenja jednaka c i u odnosu na referentno tijelo K'. Isto je sa svjetlosnom zrakom koja se širi i u nekom po volji drugom smjeru. Tome se dakako ne treba čuditi, jer su jednadžbe Lorentzovih transformacija izvedene naime s tog stanovišta.“ (kraj citata Ajnštajnovog teksta).
Nedeljko, sve pokušavam da izvedem zaključak da ovakve stavove izvodiš iz nekih drugih razloga i ciljeva, a ne iz ne znanja! Evo, ni Ajnštajn nije uočio "Nedeljkovo vrijeme":
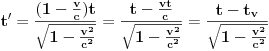
U svojoj knjizi "Teorijska fizika I dio" (na strani 425.) I. Supek piše:
„Između obaju sustava postoji dakle relacija:
(8) x' = k (x – vt).
Možemo se postaviti na stajalište da crtani sustav miruje, a necrtani se prema njemu kreće, x-koordinata necrtanog sustava bit će izražena na isti način sa x' i t', samo što ispred brzine dolazi protivan predznak, jer se necrtani sustav prema crtanom kreće u protivnom smjeru:
(9) x = k (x' + vt').
„Konstantu k možemo izračunati iz uvjeta da se svjetlosni signal u oba sustava širi s jednakom brzinom. Pustimo u početnom momentu t = t' = 0 signal iz izhodišta obaju sustava. U jednom sustavu opisuje širenje signala jednadžba:
x = ct, a u drugom x' = ct'. Uvrstimo to u jednadžbe (8) i (9):
ct' = k (ct – vt)
ct = k (ct' + vt').
Odlučno je da smo stavili istu konstantu c. Pomnožimo lijeve i desne strane ovih jednadžbi:
 [Ovu poruku je menjao Sprečo dana 30.05.2012. u 13:19 GMT+1]
[Ovu poruku je menjao Sprečo dana 30.05.2012. u 13:19 GMT+1]