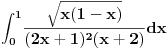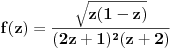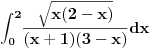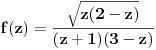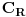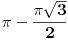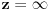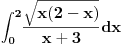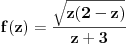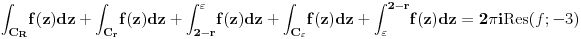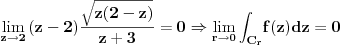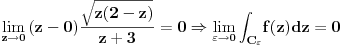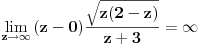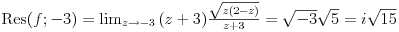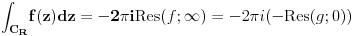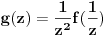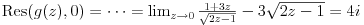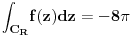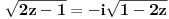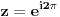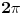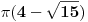Pošto mi je mozak već duže vreme kao rešeto, ne zameri ako se ne sećam
najbolje stvari vezanih za kompleksnu (posebno kad se uzme u obzir kako sam
polagao predmet vezan za istu). Pokušaću da pomognem, ali ne verujem da ću
umeti.
U vezi rešenja koje si naveo na kraju - da li je u pitanju prvi ili drugi
integral?
Napravio sam mali pokušaj sa onim drugim integralom, i dobijem rešenje
nula, koje mi nekako izgleda sumnjivo.
Evo kako se meni čini da bi se to moglo raditi.
i) Imaš ogromnu spoljnu konturu za koju bi trebalo da se može dokazati da
je integral po njoj jednak nuli. Koliko se sećam, kod iole "normalnih"
funkcija, ta kontura je bila krug pa se pomoću modula pokaže da je vrednost
integrala manja od nečega što teži nuli. U ovom slučaju se možda može
iskoristiti da je
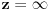
nula podintegralne funkcije (ovde
veliki znak pitanja), pa bi to moglo da znači da je u beskonačnosti (ma šta
ona bila) integral po velikoj konturi (mislim na spoljni deo složene
konture) jednak nuli "iz opravdanih razloga". (ovde oprez, pošto postoji
realna opasnost da grešim silno).
ii) Kako ti ostaju integrali po malim konturama i šetnje po realnoj osi
tamo-amo (što bi trebalo da se potire), njih (mislim na integrale po malim
konturama) nađeš uz pomoć reziduuma (oni po krugovima oko tačaka grananja
bi trebalo da su nula), a nepoznati integral izraziš preko vrednosti
integrala po celoj konturi (znaš da je nula, pošto ona u ovom slučaju ne
obuhvata singularitete) i vrednosti integrala na ostalim delovima složene
konture.
(pretpostavljam da je tvoj komentar na ovo poslednje: "Kaži mi nešto što ne
znam.")
E, po ovom receptu ja dobijem da je integral u drugom zadatku jednak nuli
(reziduumi u -1 i 3 su suprotnih znakova, pa se skrate).
Za prvi zadatak je neophodno malo više računanja, pošto je valjda potrebno
naći izvod prilikom računanja jednog od reziduuma, pa je moguće da sam
napravio grešku, pošto ni tu nisam dobio ono što si ponudio na kraju.
Kao što se vidi iz načina na koji sam pokušao da radim ove zadatke, smatram
da nema razlike da li ti obuhvatiš one polove ili ne. Ti ćeš ih svakako
zaračunati, bilo tako što ćeš imati složenu konturu u kojoj nemaš
singulariteta a pomoću njih naći vrednost integrala na onim kružićima (koji
su deo one složene konture), ili tako što ih nećeš obaviti malim krugovima,
ali ćeš ih zaračunati u vrednost integrala po složenoj konturi, pošto u tom
slučaju unutar nje imaš singularitete.
CAUSHYjeva teorema o residumima, kompleksna integracija multiformne funkcije
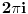, a u rešenju stoji samo nula i to bez računanja, a sa obrazloženjem "zbog osobine aditivnosti integrala", što mi uopšte nije jasno, jer u svakom slučaju se kontura vraća na početak, pa se ipak residumi računaju, a ovde samo tako. Napominjem da sam tačno proračunao residume (limese), jer se isti javljaju kao rešenje pri korišćenju JORDANovih lema ...
Re: CAUSHYjeva teorema o residumima, kompleksna integracija multiformne funkcije
), na ispitu je pala blaga modifikacija ovog zadatka ! Evo ga:
