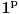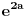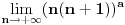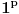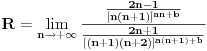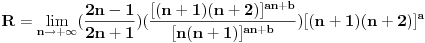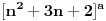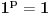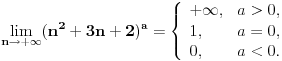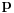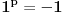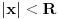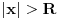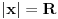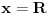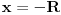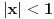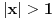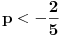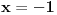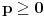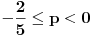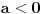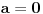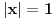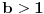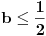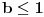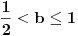Dakle, prvi red apsolutno konvergira za
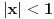
, a divergira za
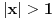
bez obzira na

. Za

apsolutno konvergira po Gausu za
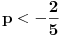
a divergira inače. Za
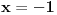
apsolutno konvergira po Gausu za
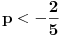
, divergira za
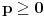
jer opšti član ne teži nuli, a za
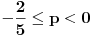
konvergira po Lajbnicu, ali po Gausu ne konvergira apsolutno, pa je ta konvergencija uslovna.
Drugi red za

konvergira apsolutno bez obzira na

, za
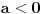
konvergira apsolutno za

i divergira za sve ostale vrednosti. Preostao je slučaj za
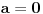
. Tada svakako konvergira apsolutno za
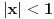
i divergira za
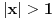
. Preostao je slučaj
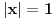
. Tada imamo apsolutnu konvergenciju akko je
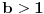
i divergenciju za
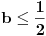
. Za

red divergira za
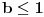
a za
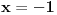
uslovno konvergira za
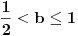
.
U realnom slučaju, stepeni red uniformno konvergira na kompaktima sadržanim u oblasti konvergencije.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
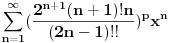
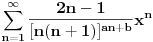
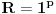 , e sta onda da uradim, jel se dalje ispituje konvergencija reda kada x uzima vrijednosti na krajevima intervala konvergencije,tj. da je
, e sta onda da uradim, jel se dalje ispituje konvergencija reda kada x uzima vrijednosti na krajevima intervala konvergencije,tj. da je 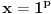 ???
???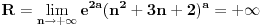




 pomoc oko dva reda
pomoc oko dva reda