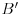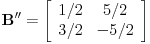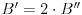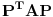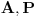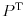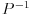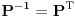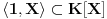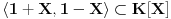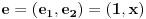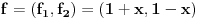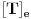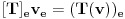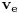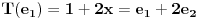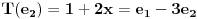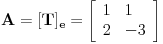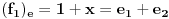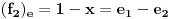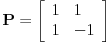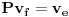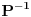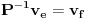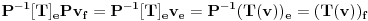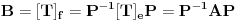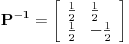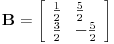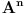Recimo da je zadan prostor M koji se sastoji iz 2x2 matrica i neka je zadan linearni operator L(A)=A^t (A transponovano). Standardne baze su (očigledno):
Code:
|1 0| |0 1| |0 0| |0 0|
e1=|0 0|, e2=|0 0|, e3=|1 0|, e4=|0 1|
Ako ove baze uvrstim u operator L(A) dobijam:
Code:
|1 0| |0 0| |0 1| |0 0|
L(e1)=|0 0|, L(e2)=|1 0|, L(e3)=|0 0|, L(e4)=|0 1|
Kako u ovom slučaju izgleda matrica linearnog operatora? Trebala bi da ima 2 vrste da bi uopšte mogla da se pomnoži sa nekom matricom iz M?
Matrica linearnog operatora se definise u odnosu na neku bazu. Ako je
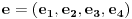 baza vektorskog prostora
baza vektorskog prostora  , onda je matrica linearnog operatora
, onda je matrica linearnog operatora 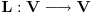 u odnosu na bazu
u odnosu na bazu  zapravo matrica
zapravo matrica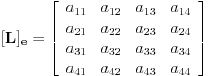
nad poljem skalara vektorskog prostora
 takva da je
takva da je 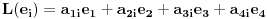 za
za 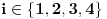 . To je definicija. U nasem slucaju je
. To je definicija. U nasem slucaju je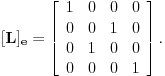




 Re: Linearna Algebra-privatni casovi potrebni
Re: Linearna Algebra-privatni casovi potrebni
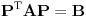
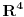
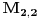
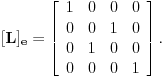
 Re: Linearna Algebra-privatni casovi potrebni
Re: Linearna Algebra-privatni casovi potrebni