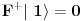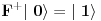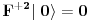Citat:
petarmMozda treba da kupis nove knjige! Nisi razmisljao o tome?
Neobavestenost nije argument!
Sasvim sam zadovoljan knjigama koje imam i mogu ti reći da su prilično relevantne.
Citat:
petarm: Ono sto je sigurno je da se Kvantna mehanika ne moze savladati iz Herbutove knjige? Ako moze reci mi sta je Rigid Hilbert space? Koji su mu elementi?
Može. Ja sam je savladao i dobio 10 kao i mnoge moje kolege, ali išao sam redovno na predavanja i vežbe, a njih nijedna knjiga ne može da zameni, inače nam fakulteti ne bi ni trebali.
Opremljeni Hilbertov prostor: je trojka
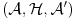
, gde je
neki Hilbertov prostor, a
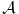
neki njegov potprostor koji je gust u
. Skup
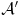
je skup svih neprekidnih linearnih funkcionala na
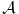
, a kada je prethodno ispunjeno, onda je
podskup
.
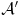
Na primer:
.
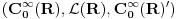
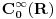
je prostor svih kvadratno integrabilnih funkcija nenultih unutar konačnog intervala.
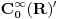
je skup svih neprekidnih linearnih funkcionala na
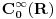
i on sam je vektorski prostor jer svaki vektor definiše linearni funkcional preko skalarnog proizvoda i obrnuto (Riesz-Frechet-ov teorem). Iz njega se izdvaja potprostor
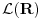
koji je zatvarač skupa
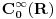
. Na taj način smo zatvorili sve skalarne proizvode i obezbedili "lepe" osobine funkcija sa kojima radimo.
E sada, sve ovo što sam ti napisao ti uopšte nije potrebno da bi se bavio kvantnom mehanikom. Primetio sam kod tebe da se previše zadržavaš na matematičkim detaljima koji nisu bitni za fizičko razumevanje problema. Zapamti, za fizičare je matematika sredstvo kojime postižemo ciljeve, a ne cilj sam po sebi.
Fermi operatori i njihovo fizicko objasnjenje
Registrovani: 0 ( 0 )
