Moja najbolja referenca je knjiga:
Probability, Random Variables and Stochastic Processes (Paperback)
by Athanasios Papoulis (Author), S.Unnikrishna Pillai (Author)
Slucajni proces mozes da posmatras kao slucajnu promenjljivu. Samo, za razliku od obicne slucajne promenjljive ciji je odredjeni ishod broj (ili najvise, konacan broj brojeva), *pojedinacan* ishod slucajnog procesa je citava funkcija f(t).
Korelacione funkcije k-tog reda su onda proseci izraza tipa f(t_1)f(t_2)...f(t_k) preko raspodele *funkcija* f(t).
Ako sada slucajni signal ubacis u LTI sistem, ovaj sistem ce svaki ishod f(t) ovog procesa da "obradi" i napravi g(t). Stoga ce koralciona funkcija na izlazu da bude <g(t_1)g(t_2)...g(t_k)> gde < > oznacava prosek preko raspodele funkcija f(t) na ulazu LTI sistema. Pri tome, ako LTI sistem opisemo impulsnim odzivom G(tau), onda:
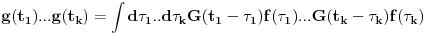
Usrednjivanjem preko raspodele funkcija f imamo:
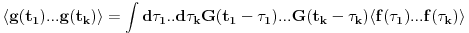
Drugim recima, ako i samo ako znamo korelacione funkcije k-tog reda na ulazu LTI sistema, znacemo i koralacine funkcije na izlazu, kao i na kombinaciji ulaza i izlaza.
Da bi se izbeglo svo ovo integraljenje po vremenu i koriscenje impulsnih odziva, citava ova prica moze da se prica i u Fourier domenu. Ovo izgleda prilicno ocigledno -- umesto da posmatramo kao instance slucajnog procesa funkcije f(t), posmatramo njihove Fourier transforme
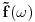
. Onda lepo kratko imamo:
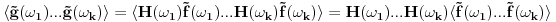
Dakle, ako znamo korelacione funkcije izlaza u Fourier domenu, korelacione funkcije izlaza mozemo naci prostim mnozenjem prenosnom funkcijom (u frekventnom domenu) LTI sistema.
Nazalost, ovo zvuci prostije nego sto u stvari jeste. Npr., kod Fourier-a se veoma brzo nailazi na beskonacnosti. Tako npr., za bilo kakav slucajan signal koji se ponasa isto u bilo kojoj tacki u vremenu (i stoga beskonacno traje!),
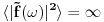
. Ova beskonacnost da se popraviti ako se posmatra signal koji traje veoma dugo (i stoga se *skoro* ponasa isto u bilo kojoj tacki u vremenu) a onda sracuna
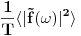
. Ova vrednost pak odgovara Fourier transformu autokorelacione funkcije drugog reda
:
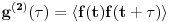
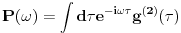
Oznaka
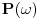
nije slucajna -- ova velicina se da relativno lako izmeriti i intuitivno fizicki interpretirati kao frekventna gustina snage signala. Razumevanja ovoga sledi medjutim tek iz malo pazljivije analize rada *fizickog* tj. realnog analizatora spektra.
Autokorelaciona funkcija
. Inace, teorija, definicije problema i uopceno klasicna teorija koja se obradjuje kroz predmet i nije toliki problem. Vise me interesuje primjena autokorelacione funkcije, spektralne gustine i kroskorelacione funkcije. Nasao sam primjer primjene u radio astronomiji ali veome sturo obradjen. Ako ima neka dobra dusa voljna pomoci bio bih zahvalan. Veliki pozdrav.
