Prvo, u pitanju je homogena linearna jednačina, koja se može lako rešiti po najvišem izvodu.
Osobina takvih jednačina je da njihova rešenja obrazuju vektorski prostor, čija je dimenzija jednaka redu jednačine, što sledi iz Pikarove teoreme o postojanju i jedinstvenosti rešenja. Dakle, ako nađemo dva linearno nezavisna rešenja bilo kojom metodom, završili smo posao. Potražićemo ga u vidu stepenog reda.
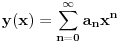
,
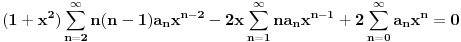
,
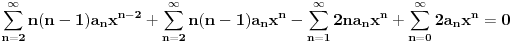
,
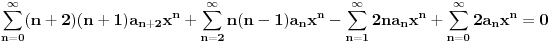
,
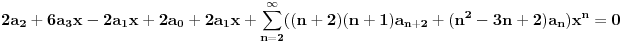
,
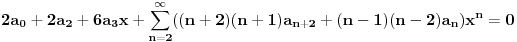
.
Odavde sledi da je
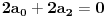
,
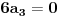
,
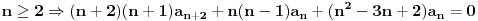
,
Dakle,
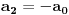
,
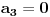
,
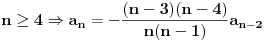
.
Indukcijom se lako dokazuje da je
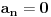
za
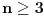
. Dakle, rešenja su oblika
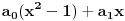
.
[Ovu poruku je menjao Nedeljko dana 22.10.2012. u 20:49 GMT+1]
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.