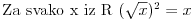Pa zavisi iz kojeg je predmeta zadatak.
Moras navesti zasto nije tacna, to jest da ne zadovoljava nesto :).
Recenica je logicki tacna ako za svaku intepretaciju ...
Pa dakle koja je ovde intepretacija, R je skup realnih brojeva, a ne kompleksnih, zar ne ?
Pa onda ...
A mozda je predmet metodika nastave, pa profesor navlaci studente da im pokaze kako su brzi i glupi :).
Tako da, eto, mozda su ljudi krenuli da dokazuju da je to tacno i da razlazu , a trebalo je samo da ...
Receniza " za svako x vazi osobina(x)" je netacna ako postoji x za koje je osobina(x) netacno.
E sada, jos malo toga, obicno se osobine ispituju na domenu racunljivosti funkcije koje postoje. Tako posto je ovde slucaj sa kvadrinm korenom koji je definisan za sve realne brojeve vece ili jednake od 0 ...
PItanje je kako li su se ljudi dogovorili.
Ali sve mi ovo lici na metodiku nastave matematike :)...
CHUPCKO