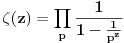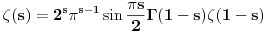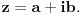[es] - Trivijalne nule Zeta funkcije

stalker
Branko Kokanovic
Beograd

Član broj: 11897
Poruke: 601
*.rcub.bg.ac.yu

Profil

^{02.06.2004. u 09:00}

Da li neko razume zasto su trivijalne nule zeta funkcije -2,-4,-6. Nikako mi, znaci, ne ide u glavu. Moze li neko da mi objasni posto nesto krupno ocigledno propustam...

Za one koji bi zeleli da pomognu, a ne znaju o cemu se radi:
Reimman zeta funkcija je definisana sa:

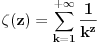
Nista prostije...z inace je kompleksan broj, ali ja pricam sada samo za realne. Postoje trivijalne i netrivijalne nule - trivijalne su -2,-4,-6... Ja, kad pokusam da zamenim to u definiciju dobijam, po starom pravilu
JEDAN KROZ NESTO NA NEGATIVNO JE NESTO NA POZITIVNO sto ce reci da mi ova suma divergira, jer su sabirci sve sami pozitivni brojevi.
Maple, however, crta lepo ovu funkciju na negativnom delu, oscilirajuci, gde su tacke preseka sa x-osom -2,-4,-6... Pokusam li da mu uradim sumu sa nekom trivijalnom nulom, javlja mi beskonacno, sto razumem, ali ne razumem sto onda svi kazu da su -2,-4,-6 nule.

P.S. Strasna funkcija, samo me mnogo nervira

^{02.06.2004. u 09:00}

Nedeljko
Nedeljko Stefanovic

Član broj: 314
Poruke: 2357
*.dial.InfoSky.Net

Profil

Re: Trivijalne nule Zeta funkcije

^{02.06.2004. u 13:44}

Rimanova zet funkcija se definiše na način koji si opisao samo za realne vrednosti z koje su veće od 1. Zatim se pokazuje da je ta funkcija analitička na intervalu (1,beskonačno), to jest da je beskonačno diferencijabilna i da se u nekoj okolini ma koje tačke u kojoj je definisana može razviti u Tejlorov red (koji u toj okolini konvergira i to baš toj funkciji). Onda nam teorija analitičkih produženja iz Kompleksne Analize garantuje egzistenciju i jedinstvenost kompleksne analitičke funkcije koja produžava tu funkciju. Tu funkciju zovemo analitičkim produženjem date funkcije. E, ona je definisana u pomenutim tačkama i u njima ima vrednost nula.

^{02.06.2004. u 13:44}

stalker
Branko Kokanovic
Beograd

Član broj: 11897
Poruke: 601
*.rcub.bg.ac.yu

Profil

Re: Trivijalne nule Zeta funkcije

^{03.06.2004. u 18:49}

1.Da li sam dobro shvatio da ova gore definicija vazi za sve kompleksne brojeve, a za realne samo >1.(ili mozda Re(z)>1 ili |z|>1)?

2.Kada vazi onda ova definicija

3.Mozes li pored ovoga da napises par reci o toj "teoriji analitickih produzenja", posto prvi put to cujem, ili neke reference na netu ako te mrzi

^{03.06.2004. u 18:49}

Nedeljko
Nedeljko Stefanovic

Član broj: 314
Poruke: 2357
*.dial.InfoSky.Net

Profil

Re: Trivijalne nule Zeta funkcije

^{05.06.2004. u 00:56}

1. Gornja definicija je primenljiva kada taj red konvergira. znači, za realne brojeve veće od jedan. U kompleksnom području se definiše preko analitičkog produženja.

2. Za realne

3. Ne mogu. To je vrlo obimna priča. Referenca je svaka dobra knjiga iz Kompleksne Analize. Dve najbolje koje sam ja čitao su "Uvod u Kompleksnu Analizu" od Šabata (na ruskom) i "Realna i Kompleksna Analiza" od Rudina (na engleskom). Obrati pažnju da Nemci ovu oblast zovu "Teorija Funkcija" ako budeš čitao na nemačkom. Na internetu nisma nikad niošta tražio na tu temu, što i dalje tebe ne sprečava da malo "proguglaš" veb.

^{05.06.2004. u 00:56}

stalker
Branko Kokanovic
Beograd

Član broj: 11897
Poruke: 601
*.rcub.bg.ac.yu

Profil

Re: Trivijalne nule Zeta funkcije

^{05.06.2004. u 09:33}

Nema nista zanimljivo o produzenjima (kako mu to dodje na engl.) Najblize cemu sam dosao je na http://planetmath.org/encyclopedia/RiemannZetaFunction.html

Mislim da ova jednacina ima veze sa tim, posto se javlja s i 1-s?

Nasao sam i elegantan euler-ov dokaz za prelazak iz prvog i drugi (sa prostim brojevima) oblik, medjutim margina mi mala da ga napisem.

Ima simbolike da je broj prve poruke koju sam postovao prost broj,a:)

^{05.06.2004. u 09:33}

Nedeljko
Nedeljko Stefanovic

Član broj: 314
Poruke: 2357
*.rcub.bg.ac.yu

Profil

Re: Trivijalne nule Zeta funkcije

^{05.06.2004. u 10:50}

Da, ja sam se očigledno prešao. Pomeniti red konvergira kad god je

. Pritom, pošto je tu n prirodan, a samim tim i realan pozitivan broj, možeš koristiti formulu

gde je

Inače, teoriju analitičkog produženja možeš naći na adresi
http://www.fact-index.com/a/an/analytic_continuation.html

^{05.06.2004. u 10:50}

filmil
Filip Miletić
Oce Technologies B.V., inženjer hardvera
Arcen, NL

Član broj: 243
Poruke: 2114
*.adsl.zonnet.nl

Jabber: filmil@jabber.org
ICQ: 36601391

Profil

Re: Trivijalne nule Zeta funkcije

^{10.06.2004. u 01:41}

Narode, natrčah na ovu vest, tip tvrdi da je dokazao Rimanovu hipotezu. Možda će vas zanimati.

f

http://zdnet.com.com/2100-1104_2-5229702.html?tag=zdfd.newsfeed

^{10.06.2004. u 01:41}

stalker
Branko Kokanovic
Beograd

Član broj: 11897
Poruke: 601
*.rcub.bg.ac.yu

Profil

Re: Trivijalne nule Zeta funkcije

^{10.06.2004. u 09:22}

Ovo je tipican tekst za npr. moju kevu. Nit sta zna o matematici, niti je zanima, ali ako se pojavi u zanimljivostima u njenim omiljenim dnevnim novinama - procitace. Ima tu svega za jedan komercijalan tekst - malo istorije, uglavnom prica sa stane, sve to zacinjeno senzacionalnoscu. Za tebe, Nedeljka i ostale (i mene) tekst je bezveze. Zakljucak je:
...nego sto su i pre znala - ga, ga, ga.

^{10.06.2004. u 09:22}

filmil
Filip Miletić
Oce Technologies B.V., inženjer hardvera
Arcen, NL

Član broj: 243
Poruke: 2114
*.decis.nl

Jabber: filmil@jabber.org
ICQ: 36601391

Profil

Re: Trivijalne nule Zeta funkcije

^{10.06.2004. u 12:08}

Na dva klika odatle, „malo“ ozbiljniji tekst: http://www.math.purdue.edu/ftp_pub/branges/riemannzeta.pdf. Ne znam šta se može uraditi sa tekstom, ali ko može i ume, neka pogleda.

f

^{10.06.2004. u 12:08}