Ne znam koju knjigu koristiš, ali njen autor očigledno koristi nestandardnu terminologiju. Standardne definicije bi bile:
1. NP problem je problem koji se može rešiti u polinomijalnom vremenu na NEDETERMINISTIČKIM mašinama.
2. NP je klasa svih NP problema.
3. NP kompletan problem je NP problem na koji je na DETERMINISTIČKIM mašinama polinomijalno svodljiv svaki drugi NP problem.
Koliko vidim ti pod NP teškim problemima podrazumevaš NP kompletne probleme, kao i one probleme koji nisu NP. Drugim rečima, kod tebe je NP težak problem isto što i problem čija je težina NAJMANJE NP. E, pa onda se tvoje pitanje svodi na to da li postoje problemi koji nisu u klasi NP, to jest oni čija te težina VEĆA od NP. Ima ih. Postoji jedna zanimljiva teoreme (zovu je speed up teorema) koja glasi:
Neka je
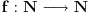
bilo koja algoritamski izračunljiva funkcija. Tada postoji podskup A skupa prirodnih brojeva takav da je problem pripadnosti tom skupu algoritamski rešiv, ali tako da za svaki program P koji rešava taj problem postoji program Q koji takođe rešava taj problem, ali tako da postoji broj m takav da za svako k>m program Q ispituje da li broj k pripada skupu A najmanje f(k) puta brže nego program P.
Ako je na primer
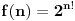
, onda će takav problem biti užasno težak i negova težina će itekako nadmašiti NP. Inače, ovu teoremu možeš naći u knjizi Computability čiji je autor Nigel Cutland.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.