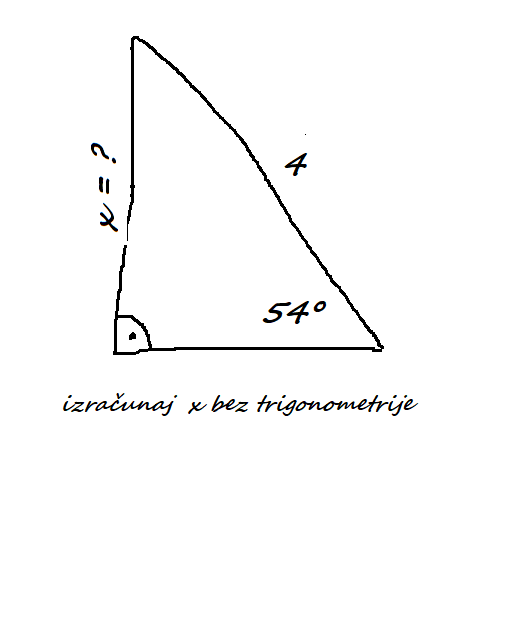
Nemam sad vremena, ali mislim da se ugao od 54 stepena podeli polupravom tako da iznad nje ostane 36 stepeni, a ispod nje 18 stepeni.
Tada se dobija jednakokraki trougao koji čine hipotenuza glavnog trougla, poluprava koja deli ugao od 54 stepena i deo katete "x".
Trougao ispod poluprave koja deli ugao od 54 stepena je zbog istih uglova sličan velikom trouglu, pa mogu da se postave jednakosti sa odnosima odgovarajućih stranica, a iz njih bi trebalo da može da se izračuna "x" eliminacijom nepoznate vrednosti za drugu katetu.
Blessed are those who can laugh at themselves, for they shall never cease to be amused.