Neka je A vrh piramide. Od vrha A to osnove piramide povučemo normalu i neka je tačka u kojoj normala prolazi kroz osnovu O. Tada je AO visina piramide.
Dalje iz tačke A nacrtamo visinu stranice piramide. Tačka u kojoj visina dodiruje bazu neka bude M i ona je tačno na polovini stranice osnove. Ovo je istovremeno i težišna linija jer se ove dve linije poklapaju kod jednakokrakog trougla. Na liniji AM se nalazi i tačka T (težište stranice) i ona deli liniju AM na duži AT i TM i imamo osobinu da je AT=2TM. Iz tačke T (koja je težište stranice piramide i istovremeno jedna od tačaka gornje osnove upisane prizme) spustimo normalu na osnovu piramide i tu tačku nazovimo N.
Sada imamo trouglove AMO i TMN koji su slični. Duž TN je visina upisane prizme i ona je jednaka 1/3 AO. Duž NO je polovina dijagonale osnove upisane prizme. Duž MO je dužine polovine stranice.
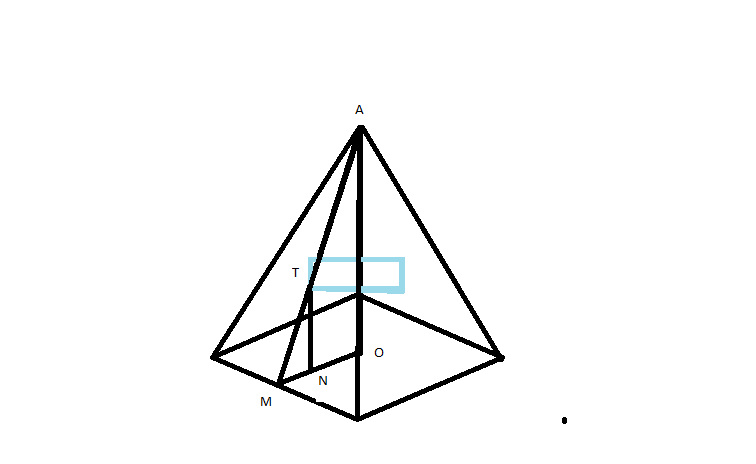
Svetlo plavi pravougaonik na slici je gornja osnova upisane prizme. Duž NO je polovina dijagonale donje osnove upisane prizme.
[Ovu poruku je menjao djoka_l dana 14.11.2016. u 09:42 GMT+1]




 Piramida i prizma
Piramida i prizma
