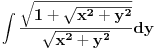Citat:
Teoreticar: Hvala na trudu :)
posle toga dobije ovo....
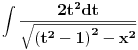
probam da ga uradim parcijalnom integracijom, ali se zakomplikuje... :)
Mislim da si lose odradio izvod ... cinimi se da treba da bude -2t^2(t^2-1) kroz ovo sto si napisao ... proveri
zatim sam isao na smenu t^2-1=z^2
pa z^2 - x^2 = p^2
i mislim da sam na kraju dobio ovako
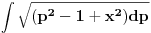
Wolfram vraca resenje van domena elementarnih funkcija, ali potrudi se da resis :)