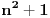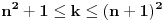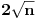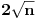|
darkosos
Darko Šoš
Beograd
Član broj: 5053
Poruke: 1131
46.240.140.*
|
Evo jedne male analize merge sorta, koja verovatno ima objašnjena po mnogim knjigama, ali eto, time sam se bavio ovih dana, pa da zapišem.
1. Najveći broj poređenja u stapanju dva sortirana niza u novi sortirani niz je jednak zbiru njihovih dužina manje jedan.
ovo će se najlakše videti iz algoritma stapanja, neka su datu nizovi A i B, i recimo da sortiramo u neopadajućem poretku
1. postavimo indekse oba niza na 1 (recimo da je indeks prvog člana niza 1), i=1, j=1
2. uporedimo A(i] sa B[j]
3. manji od ta dva stavimo u rezultujući niz, i pomerimo indeks onog niza čiji je element manji (ako povećanje za jedan ne prelazi dužinu niza)
4. ponavljamo 2. 3. dok nismo došli ili do kraja niza A ili do kraja niza B
5. ostatak (ako ga ima, a može biti samo na jednom od nizova) dodamo na formirani niz
U najgorem slučaju je i jednako dužini niza A a j dužini niza B. U svakom koraku, (osim u prvom) smo uradili jedno povećanje i ili j, i jedno poređenje. Odavde se vidi da je broj poređenja jednak i+j-1, dakle koliko pomeranja po nizovima toliko i provera, osim u prvom koraku kada imamo jednu proveru, a postavljanje oba indeksa.
Kako bi to izgledalo za niz koji je Milan (zzzz) dao? Podnizove 2,7,9,15,22 i 1,8,10,11,25 bi dakle mogli da stopimo u 5+5-1 = 9 koraka!
Naravno, generalno, stapanja u ovom algoritmu ne mora da bude samo dva, i postavlja se pitanje da li ima neke veze kojim redom vršimo stapanja? Ako smo recimo razbili skup na sortirane podnizove od 4, 3, 2, 1 element (mislim na nešto tipa [a,b,c,d], [e,f,g], [h,i], [j]), kako izvršiti stapanja? Hajde baš navedenim redom:
4+3-1 = 6 poređenja, sa rezultujućim nizom od 7 elemenata
7+2-1 = 8 poređenja, 9 el.
9+1-1 = 9 poređenja, 10 el., što daje ukupno 23 poređenja. Može li bolje?
Da, ako krenemo od manjih podnizova, redosledom 1, 2, 3, 4 elementa:
1+2-1 = 2:3 (2 por., 3 el.)
3+3-1 = 5:6
6+4-1 = 9:10, što daje samo 16 poređenja!
Ova razlika se može objasniti na sledeći način: svaki put stapamo dva podniza, i u svakom koraku se vrši kumulativno stapanje sa narednim. Tako oni koji su ranije stopljeni više puta učestvuju u narednim stapanjima, pa bi taktika bila da se prvo stapaju manji podnizovi pa sve veći. Uostalom, rezultat se dobija sabiranjem parcijalnih suma, umanjenim za jedan. U slučaju 4,3,2,1 to je 7-1 + 9-1 + 10-1 = 6+8+9, a u slučaju 1,2,3,4 to je 3-1 + 6-1 + 10-1 = 2+5+9.
Naravno, originalni merge algoritam ne radi ovako, već rekurzivno lomi niz na podjednake delove (za paran broj elemenata su isti, za neparne je jedan veći za jedan), pa se stapanje vrši uvek na najnižem nivou i time obezbeđuje optimalnost (ovo nisam proverio, ali tako izgleda). Ali, ovde je priča o tome da nemamo slepo deljenje niza, već neko koje nam kasnije može obezbediti bolje rezlutate. Iako slepo deljenje niza ima tu prednost što ne košta ništa, makar ne u smislu broja poređenja.
Ovo je neki odgovor na pitanje šta bi radili ako bi imali te sortirane podnizove. Drugi deo priče je kako doći do njih i koliko to košta? Ispisao sam brdo primera i nisam došao do zadovoljavajućeg rešenja. Traženje maksimalnog sortiranog podniza je preskupo.
Natural merge algoritam bi mogao da se poboljša sortiranjem run-ova, od manjeg ka većem, ili stapanjem uvek dva trenutno najmanja. Recimo run-ove 2, 2, 2, 2, 5 je bolje spojiti 2 i 2 (3:4), 2 i 2 (3:4), 5; 4 i 4 (7:8), 5; 8 i 5 (12:13) nego ići redom 2 i 2 (3) i 2 (5) i 2 (7) i 5 (12). Opet, overhead je traženje najmanjih, ali na duže staze (odnosno veće nizove) mislim da bi ovo dalo rezultate.
S' druge strane, traženjem sortiranih podnizova, ali od elemenata koji ne moraju biti uzastopni (u natural merge algoritmu se gledaju samo uzastopni), možda može da se nešto dobije, iako ne tako lako. Ovaj post je već predugačak pa ću ovde stati.
[Ovu poruku je menjao darkosos dana 18.07.2014. u 19:49 GMT+1]
|
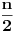 kada je n parno, odnosno
kada je n parno, odnosno 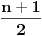 kada je n neparno, koji je sortiran - bilo neopadajuce ili nerastuce
kada je n neparno, koji je sortiran - bilo neopadajuce ili nerastuce



 Minimalna duzina najveceg sortiranog podniza
Minimalna duzina najveceg sortiranog podniza