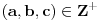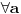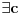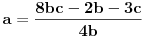mislim da sam uspeo da oborim tezu. ide ovako: obe strane mozemo pomnoziti sa 2 i dobijamo
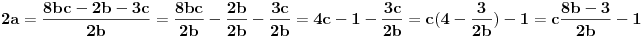
jedinicu premestimo sa desne na levu stranu i dobijemo
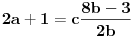
ovim se u odnosu na pocetnu postavku nista ne menja, jer dobijamo izraz za neparan broj na levoj strani, i onda imamo identicnu tvrdnju "za svako
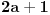
uvek postoje neki
i
za koje je jednacina tacna".
kako je
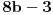
uvek neparno a
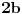
uvek parno, to onda izraz
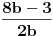
nikako ne moze biti ceo broj, vec mora biti razlomak. da bi se ispunio uslov da je
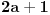
ceo broj, onda
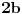
mora biti jednako
, ili
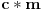
, gde je
neki ceo broj.
a kako vidimo da je
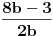
rastuci niz kada
ide od
do beskonacno, onda odmah za prva dva clana niza, kada je
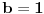
i
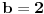
, vidimo da je
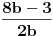
jednako u prvom slucaju
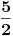
a u drugom
.
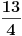
u tom slucaju minimalne vrednosti
su
i
, tako da dobijamo da je izraz na levoj strani
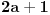
jednak
, i
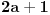
jednak
.
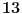
za te vrednosti, u prvom slucaju
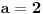
, a u drugom
.
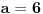
tako da ne mozemo dobiti
koje je izmedju
i
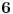
tj a za vrednosti
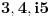
, i samim tim je tvrdnja opovrgnuta.
evenutalno neko neku ideju...
Registrovani: 1 ( misamilanovic )