[es] - Kružnica - dve tačke i prava

Nepoznat covek
Student

Član broj: 296039
Poruke: 74
*.dynamic.isp.telekom.rs.

+4 Profil

^{02.04.2012. u 19:51 - pre 160 meseci}

Napisati jednačinu kružnice koja sadrži tačke M(10,9) N(4,3), a centar joj je na pravoj: 2x-3y+19=0.
Pomoć. Radim već pola sata zadatak drugu, ali davno beše, pozaboravljao sam..

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
95.180.54.*

+64 Profil

Re: Kružnica - dve tačke i prava

^{02.04.2012. u 20:06 - pre 160 meseci}

U opstu jednacinu kruznice

zameni date tacke a cenatar (p,q) zadovoljava jednacinu date prave.

Odgovor na temu

Nepoznat covek
Student

Član broj: 296039
Poruke: 74
*.dynamic.isp.telekom.rs.

+4 Profil

Re: Kružnica - dve tačke i prava

^{02.04.2012. u 20:15 - pre 160 meseci}

e, to me je bunilo... kako da se odredi da li data tačka zadovoljava uslov?

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
95.180.54.*

+64 Profil

Re: Kružnica - dve tačke i prava

^{02.04.2012. u 20:19 - pre 160 meseci}

Mislis da pripada pravoj? Pa bre 2p-3q+19=0.

Odgovor na temu

Nepoznat covek
Student

Član broj: 296039
Poruke: 74
*.dynamic.isp.telekom.rs.

+4 Profil

Re: Kružnica - dve tačke i prava

^{02.04.2012. u 20:23 - pre 160 meseci}

Uh bre..

Smejem se samom sebi trenutno

Hvala ti

Odgovor na temu

Sprečo
penzioner

Član broj: 27004
Poruke: 1229
31.176.192.*

+33 Profil

Re: Kružnica - dve tačke i prava

^{09.04.2012. u 08:43 - pre 159 meseci}

Još teže bi ti bilo da si učio po ovom udžbeniku:

Vojislav Mihailović, napisao je 1964.g. udžbenik – Geometrija – za drugi razred gimnazije prirodno-matematičkog smjera (recenzenti: Zdravko Mihailović i Olga Mitrinović).
U navedenom udžbeniku, na strani 39. piše:
Definicija 10. Skup svih tačaka u jednoj ravni podjednako udaljenih od jedne tačke te ravni naziva se krug.
Da se ne radi o „štamparskoj grešci“ napomenut ću da u cijelom udžbeniku (148 stranica) kružnica nije pomenuta ni jedan jedini put. Za navedene matematičare – kao da taj pojam i ne postoji!?

Odgovor na temu

Sonec

Član broj: 284879
Poruke: 892

+332 Profil

Re: Kružnica - dve tačke i prava

^{09.04.2012. u 11:33 - pre 159 meseci}

Nedeljko ti je vec odgovorio. Evo, da budemo precizniji:

Citat:

Neka je

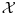
pramen pravih i

proizvoljna tacka u ravni

tog pramena koja ne pripada svim pravama pramena

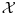
. Skup svih tacaka ravni

, osnosimetricnih tacki

u odnosu na prave pramena

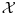
cemo zvati epicikom i obelezavacemo ga sa

.
Ako je

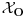
pramen konkurentnih pravih, epicikl

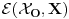
cemo zvati krugom. Tacku

cemo zvati sredistem ili centrom toga kruga, a duz

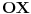
njegovim poluprecnikom ili radijusom. Krug cemo obelezavati i sa

U toj oznaci

je srediste, a

poluprecnik kruga

. Neposredno se dokazuje da krug

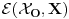
istovetan sa skupom svih tacaka

ravni kojoj pripada, takvih da je

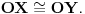
(str. 135)
................................................................................
................................................................................
Unijom kruga i njegove unutrasnjosti cemo zvati i kruznom povrsi, a sam krug cemo ponekad zvati i rubom te povrsi. (str. 138)

Zoran Lucic, Euklidska i hiperbolicka GEOMETRIJA

Takodje, na 312 strana se nigde ne pominje termin kruznica. Ne vidim neki problem zbog toga.

Leonardo da Vinči

Nema istine u onim naukama u kojima se matematika ne primenjuje.

Milorad Stevanović

Bog postoji zato sto je matematika neprotivurečna.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8714
*.3gnet.mts.telekom.rs.

+2802 Profil

Re: Kružnica - dve tačke i prava

^{09.04.2012. u 15:58 - pre 159 meseci}

Sprečo, problem sa tom definicijom kruga je što to konstantno rastojanje može biti i nula, tj. nije isključeno definicijom, a jedna tačka se ipak ne smatra krugom.

Kod Lučića se ono što se inače zove krug zove kružna površ, a ono što se inače zove kružnica se zove krug.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu