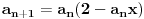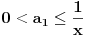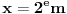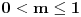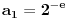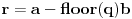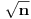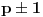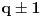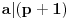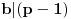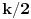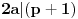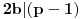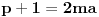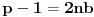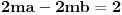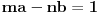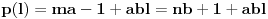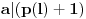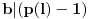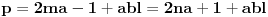RSA - kriptografija javnim ključem
Neka je
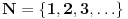 skup prirodnih brojeva i
skup prirodnih brojeva i 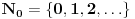 skup prirodnih brojeva sa nulom. Za par prirodnih brojeva se kaže da su uzajamno prosti ako ne postoji prirodan broj veći od 1 koji deli svaki od njih. Ojlerova funkcija
skup prirodnih brojeva sa nulom. Za par prirodnih brojeva se kaže da su uzajamno prosti ako ne postoji prirodan broj veći od 1 koji deli svaki od njih. Ojlerova funkcija  je funkcija koja svakom prirodnom broju pridružuje broj prirodnih brojeva ne većih od njega, a koji su uzajamno prosti sa njim. Primera radi, od brojeva 1,...,9, sa 9 su uzajamno prosti 1,2,4,5,7 i 8. Dakle, ima ih 6, pa je
je funkcija koja svakom prirodnom broju pridružuje broj prirodnih brojeva ne većih od njega, a koji su uzajamno prosti sa njim. Primera radi, od brojeva 1,...,9, sa 9 su uzajamno prosti 1,2,4,5,7 i 8. Dakle, ima ih 6, pa je 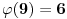 . Za ovu funkciju dokayuje se da za ma koje uzajamno proste brojeve
. Za ovu funkciju dokayuje se da za ma koje uzajamno proste brojeve  i
i  važi
važi 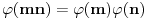 (ova osobina se zove multiplikativnost), kao i da je
(ova osobina se zove multiplikativnost), kao i da je 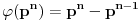 za ma koji prost broj
za ma koji prost broj  i prirodan broj
i prirodan broj  , odakle je u opštem slučaju
, odakle je u opštem slučaju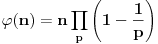 ,
,pri čemu se proizvod izmima po svim prostim deliteljima
 broja
broja  uzimajući svaki prost delitelj po jedanput.
uzimajući svaki prost delitelj po jedanput.RSA algoritam je zasnovan na Ojlerovoj teoremi, koja kaže da je za ma koje uzajamno proste prirodne brojeve
 i
i  broj
broj 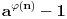 deljiv sa
deljiv sa  . Stoga brojevi
. Stoga brojevi 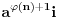
 daju isti ostatak pri delenju sa
daju isti ostatak pri delenju sa  .
.U našem slučaju će biti
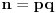 proizvod različitih prostih brojeva
proizvod različitih prostih brojeva  i
i  , odakle će biti
, odakle će biti 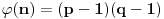 . Ukoliko su
. Ukoliko su  i
i  prirodni brojevi za koje je
prirodni brojevi za koje je 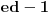 deljivo sa
deljivo sa 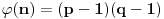 , onda će za ma koji prirodan broj
, onda će za ma koji prirodan broj  manji od
manji od  i uzajamno prost sa njim ostatak pri delenju broja
i uzajamno prost sa njim ostatak pri delenju broja 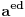 sa
sa  biti jednak
biti jednak  .
.Par
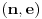 je jedan deo ključa, koji zovemo tajnim, a par
je jedan deo ključa, koji zovemo tajnim, a par 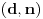 je drugi deo kluča, koji zovemo javnim. Poruka je bilo koji prirodan broj
je drugi deo kluča, koji zovemo javnim. Poruka je bilo koji prirodan broj 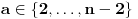 . Svaki niz bitova možemo shvatiti kao prirodan broj čiji je to binarni zapis. Ako
. Svaki niz bitova možemo shvatiti kao prirodan broj čiji je to binarni zapis. Ako  ima 2049 bitova, i veći je od
ima 2049 bitova, i veći je od 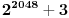 , onda poruci maksimalne dužine 2048 bita shvaćenoj kao prirodan broj, možemo dodati 2 i dobiti broj
, onda poruci maksimalne dužine 2048 bita shvaćenoj kao prirodan broj, možemo dodati 2 i dobiti broj  za šifriranje. Duža poruka se u tom slučaju može podeliti na blokove od po 2048 bita, nakon čega se šifrira svaki blok ponaosob.
za šifriranje. Duža poruka se u tom slučaju može podeliti na blokove od po 2048 bita, nakon čega se šifrira svaki blok ponaosob.Broj
 šifriramo tako što izračunavamo ostatak od
šifriramo tako što izračunavamo ostatak od 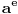 pri delenju sa
pri delenju sa  . Rezultat
. Rezultat  dešifrujemo tako što izračunamo ostatak pri delenju
dešifrujemo tako što izračunamo ostatak pri delenju 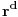 po modulu
po modulu  . Ukoliko je broj
. Ukoliko je broj  uzajamno prost sa
uzajamno prost sa  , rezultat će biti
, rezultat će biti  , pa umanjivanjem za 2 dobijamo originalnu poruku. To smo i očekivali, jer kada se šifrovana poruka dešifruje, treba da se dobije originalna poruka. To će se svakako desiti ako je
, pa umanjivanjem za 2 dobijamo originalnu poruku. To smo i očekivali, jer kada se šifrovana poruka dešifruje, treba da se dobije originalna poruka. To će se svakako desiti ako je  bilo uzajamno prosto sa
bilo uzajamno prosto sa  . Ojlerova funkcija nam kaže da među
. Ojlerova funkcija nam kaže da među 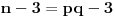 mogućih poruka problem može nastati sa njih
mogućih poruka problem može nastati sa njih 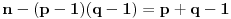 , odnosno da je verovatnoća za to oko
, odnosno da je verovatnoća za to oko 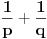 za velike proste brojeve
za velike proste brojeve  i
i  , što je rizik koji se može zanemariti.
, što je rizik koji se može zanemariti.Sada prelazimo na detaljnije objašnjenje svih koraka. Da bi implementacija bila brza, treba koristiti algoritam množenja zasnovan na brzoj Furijeovoj transformaciji (FFT) i ovde neće biti izložen, jer je tekst i bez toga preopterećen matematikom.
1. Stepenovanje
Stepenovanje realizovano po definiciji, uzastopnim množenjem, je neprihvatljivo sporo. Stoga se za izračunavanje
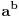 po zadatom modulu
po zadatom modulu  može realizovati sledećom rekurentnom funkcijom:
može realizovati sledećom rekurentnom funkcijom:int power(int a, int b, int n) {
if (b == 0)
return 1;
int ret = pow(a, b >> 1, n);
if (b & 1)
ret *= a;
return ret % n;
}
2. Generisanje prostih brojeva
Da bismo dobili ključeve širine 4096 bita, trebaju nam dva prosta broja sa po 1024 binarne cifre. Oni se tipično generišu tako što se generišu nasumični brojevi željene širine, a potom testira da li su prosti. Nažalost, vrlo je teško utvrditi da je neki broj sigurno prost, pa se koriste razni testovi pseudoprimalnosti, među koje spada Miler-Rabinov test. Ako neki broj prođe taj test, on je najverovatnije prost (jako je mala verovatnoća da je složen), a ako ga ne prođe, sigurno je složen. Algoritam sledi.
bool is_pseudoprime(int p, int b) {
int d = p - 1;
int s = 0;
while (d & 1 == 0) {
d >>= 1;
s = s + 1;
}
int a = power(b, d, p - 1);
if (a == 1 || a == -1)
return true;
for (int i = 1; i < s; i = i + 1) {
a = a * a % (p - 1);
if (a == -1)
return true;
}
return false;
}
int pseudoprime(int max) {
int p;
while (true) {
p = rand() % max;
if (p < 2)
continue;
if (is_pseudoprime(p, 2) == false)
continue;
if (is_pseudoprime(p, 3) == false)
continue;
if (is_pseudoprime(p, 5) == false)
continue;
if (is_pseudoprime(p, 7) == false)
continue;
if (is_pseudoprime(p, 11) == false)
continue;
break;
}
return p;
}
Funkcija za testiranje pseudoprimalnosti zahteva osnovu
 kao argument. Ovde je primalnost testirana za pet prostih osnova. Funkcija za generisanje pseudoprostog broja generiše broj u opsegu
kao argument. Ovde je primalnost testirana za pet prostih osnova. Funkcija za generisanje pseudoprostog broja generiše broj u opsegu 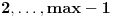 .
.3. Generisanje brojeva e i d
Jedan od ovih brojeva se moze izabrati nasumicno, na primer e, a drugi generisati sledecim algoritmom:
bool extednded_euclid(int m, int n, int &u, int &v) {
if (m < 0 || n < 0) {
if (extended_euclid(abs(m), abs(n), u, v) == false)
return false;
if (m < 0)
u = -u;
if (n < 0)
v = -v;
return true;
}
if (m < n)
return extednded_euclid(n, m, v, u);
if (n == 0)
return false;
int q = m / n;
int r = m - q * n;
int t;
if (extednded_euclid(n, r, t, u) == false)
return false;
v = t - q * u;
return true;
}
void generate_keys(int max, int &n, int &e, int &d) {
while (true) {
int p = pseudoprime(max);
int q = pseudoprime(max);
if (p == q)
continue;
n = p * q;
int fi_n = (p-1)*(q-1);
while(true) {
int e = rand() % fi_n;
int d, t;
if (extednded_euclid(fi_n, e, t, d) == false)
continue;
d = d % fi_n;
if (d < 0)
d += fi_n;
break;
}
break;
}
}
4. Funkcije za enkripciju i dekripciju
int encrypt(int message, int n, int e) {
return power(message + 2, e, n);
}
int decrypt(int message, int n, int d) {
return power(message, d, n) - 2;
}
Zasad toliko.
[Ovu poruku je menjao Mihajlo Cvetanović dana 16.03.2011. u 16:26 GMT+1]




 Teorijske osnove RSA algoritma
Teorijske osnove RSA algoritma