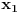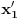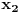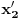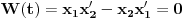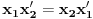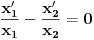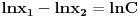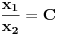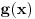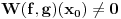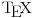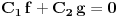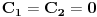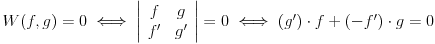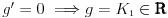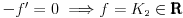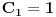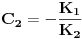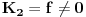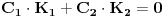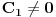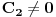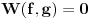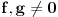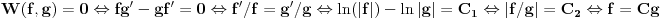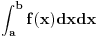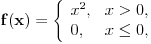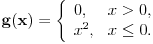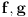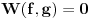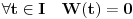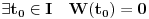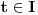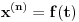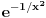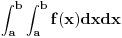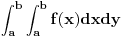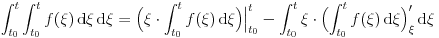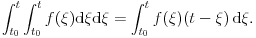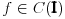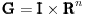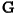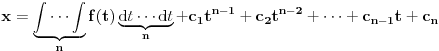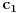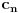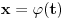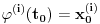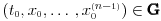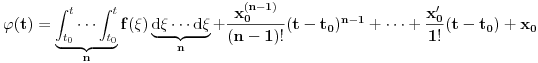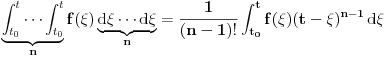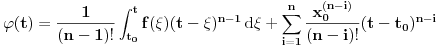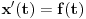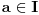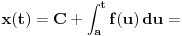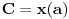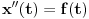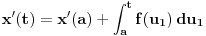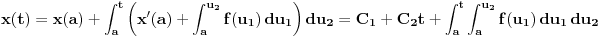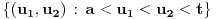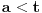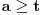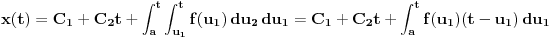Molim? Kakvo je to pitanje? Šta ti očekuješ od Julkine knjige? Sećam se kada je preko skupa nula rešenaj dif. j-ne dokazivala da su funkcije A*sin(t) i B*sin(t) linearno nezavisne. Posle je popravila to, a dodala druge "bisere".
Šalu na stranu, nećeš naći dif. j-nu oblika y''(x)=u(x,y(x),y'(x)), gde je f-ja u neprekidno diferencijabilna po trećem argumentu, a čija su rešenja funkcije f i g. Štaviše, f i g nemaju drugi izvod u tački 0. Satim nećeš naći ni odgovarajuću linearnu dif. j-nu drugog reda kakvu zahteva ta teorema.
Mogu se napakovati primeri sa beskonačno diferencijabilnim funkcijama (zameni

sa
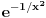
), ali će koordinatni početak biti singularna tačka eventualne dif. j-ne. Ne odnosi se to na linearnu nezavisnost bilo kakvog sistema funkcija, već taj sistem funkcija mora biti rešenje iste linearne diferencijalne jednačine.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
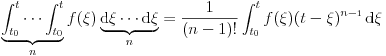 ? Konkretno, interesuje me samo ovaj prelaz:
? Konkretno, interesuje me samo ovaj prelaz: 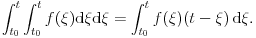
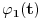 ,
,  ,
, 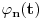 jednačine
jednačine 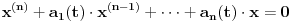 moraju biti linearno zavisna? Pol Dokins kaže da dve linearno nezavisne funkcije mogu da imaju
moraju biti linearno zavisna? Pol Dokins kaže da dve linearno nezavisne funkcije mogu da imaju 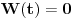 , tj.:
, tj.: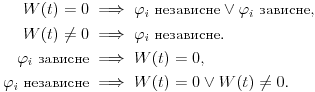




 Diferencijalne, vronskijan i (ne)zavisnost, itd.
Diferencijalne, vronskijan i (ne)zavisnost, itd.