Pa evo ovako:
Prvo treba da prepoznas kako bi sumirao ovaj red.Ovde se nekako nazire da treba da namestis drugi izvod funkcije. Kada to uradis onda imas sumu geometrijskog reda koju mozes lako da saberes.
Znaci:
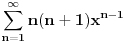
Ako bi napravio drugi izvod funkcije
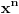
onda stepen treba da ti bude n-2 a tebi je n-1. Znaci treba da nastelujes n-2 a da ne poremetis vrednost sume.
Malo mucnes glavom i skontas da je to
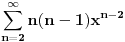
.
Provera (uzmes prva 2-3 clana):
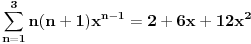
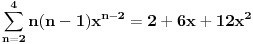
Znaci da je namestanje ok (primeti da je sad prvi clan za n=2 a ne za n=1)!
Ovo
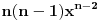
je drugi izvod funkcije
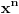
.
Znaci,
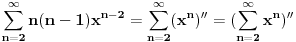
E sad si dobio sumu geometrijskog reda koja pocinje od 2. Suma geom. reda racunas po formuli
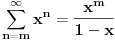
Znaci
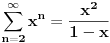
I sad jos odradis drugi izvod i dobijes:
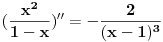
A to sto je petarm napisao da pocinje od nule nije greska jer je drugi izvod elemenata sume (n=0 i n=1) jednak nuli pa se suma nece promeniti.
Eureka!
MILAN DJUKIC
D J U K A