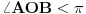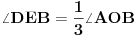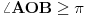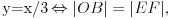Metod je vrlo jednostavan, i tako ću pokušati i da ga izložim:
1) Ukoliko je ugao veći od
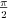 oduzmemo
oduzmemo 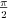 dovoljan broj puta da bi dobili oštar ugao koji dalje delimo, a ugao od
dovoljan broj puta da bi dobili oštar ugao koji dalje delimo, a ugao od 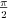 je lako podeliti na 3 dela, jer je svaki deo
je lako podeliti na 3 dela, jer je svaki deo 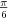 i moguće ga je konstruisati.
i moguće ga je konstruisati.2) Na oba kraka ugla
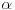 nanesemo tri puta proizvoljnu dužinu
nanesemo tri puta proizvoljnu dužinu 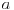 dobijajući tako tačke
dobijajući tako tačke 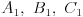 na jednom i
na jednom i 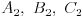 na drugom kraku ugla, repektivno.
na drugom kraku ugla, repektivno.3) Podelimo kružni luk
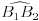 na dva dela. Neka je sredina tačka
na dva dela. Neka je sredina tačka 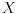 .
.4) Neka je
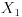 tačka na luku
tačka na luku 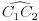 takva da je
takva da je 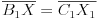 . Dokazaću da je
. Dokazaću da je 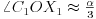 .
.Dokaz:
Ukoliko je
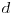 dužina tetive koja odgovara centralnom uglu
dužina tetive koja odgovara centralnom uglu 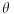 u krugu poluprečnika
u krugu poluprečnika 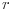 , poznato je da važe sledeće formule:
, poznato je da važe sledeće formule: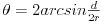
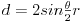
Dalje je računica prosta:
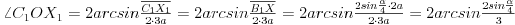
Da bismo dobili relativnu grešku u odnosu na početni ugao, oduzećemo vrednost ovog ugla od trećine vrednosti početnog, i to sve podeliti sa početnim. Drugim rečima, greška je vrednost funkcije:
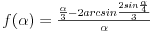
Grafik te funkcije izgleda ovako:
Kao što vidimo, što je ugao veći veća je i greška, i teži ka 0.005 (jer smo pretpostavili da je ugao oštar), što je približno jednako 0.5%. Ovo se može još smanjiti tako što u prvom koraku ne posmatramo uglove manje od
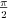 nego od
nego od 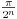 , jer se svaki ugao oblika
, jer se svaki ugao oblika 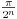 može tačno podeliti na 3 dela (dobije se
može tačno podeliti na 3 dela (dobije se 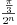 . što je moguće konstruisati), i možemo dobiti proizvoljno malu grešku za dovoljno veliko
. što je moguće konstruisati), i možemo dobiti proizvoljno malu grešku za dovoljno veliko 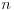 .
.



 Trisekcija ugla
Trisekcija ugla