[es] - Formula za izbacivanje svih prostih brojeva

Teoreticar
Galileo Galilej
Tuzla

Član broj: 129740
Poruke: 161
89.146.171.*

+1 Profil

Formula za "izbacivanje" svih prostih brojeva

^{11.11.2008. u 23:57 - pre 200 meseci}

Poznato je da ne postoji formula pomoću koje se mogu dobiti svi prosti brojevi...
Ima li ovdje nekih pomaka ili pribliznih rjesenja...

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dynamic.sbb.rs.

+2801 Profil

Re: Formula za "izbacivanje" svih prostih brojeva

^{12.11.2008. u 08:03 - pre 199 meseci}

Postoji polinom stepena 25 sa 26 promenljivih i sa celim koeficijentima takav da je skup pozitivnihvrednosti tog polinoma za celobrojne vrednosti promenljivih jednak skupu prostih bojeva.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

Teoreticar
Galileo Galilej
Tuzla

Član broj: 129740
Poruke: 161
91.191.35.*

+1 Profil

Re: Formula za "izbacivanje" svih prostih brojeva

^{12.11.2008. u 10:39 - pre 199 meseci}

Bio bi ti veoma zahvalan ako bi nam napisao taj polinom - ako si u mogućnosti, veoma me zanima.
Postojel jos neke pojedinosti u vezi toga...

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dynamic.sbb.rs.

+2801 Profil

Re: Formula za "izbacivanje" svih prostih brojeva

^{12.11.2008. u 10:55 - pre 199 meseci}

Trenutno mi nije pri ruci knjiga "Hilbertovi problemi i logika" u kojoj je taj polinom napisan, ali cu se potruditi da ga okacim.

Ako ti ovo treba zbog kriptografije, onda ti je ovaj polinom lose resenje.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

Teoreticar
Galileo Galilej
Tuzla

Član broj: 129740
Poruke: 161
89.146.187.*

+1 Profil

Re: Formula za "izbacivanje" svih prostih brojeva

^{12.11.2008. u 11:34 - pre 199 meseci}

Ok, hvala ti mnogo...strasno bi me interesovao taj polinom.Ne treba mi za kriptografiju.

Na koji način bi se onda menjale vrednosti promenljivih u tom polinomu (cele vrednosti)?

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
93.86.158.*

+2801 Profil

Re: Formula za "izbacivanje" svih prostih brojeva

^{12.11.2008. u 17:56 - pre 199 meseci}

Zameniš promenljive bilo kojim celim brojevima, izračunaš vrednost izraza, pa ako dobiješ pozitivnu vrednost, onda je to sigurno prost broj, a ako vrednost nije pozitivna, onda jednostavno nisi imao sreće - ne znaš ni da li je prost ni da li je složen. No, svaki prost broj se može dobiti kao pozitivna vrednost tog polinoma za neke celobrojne vrednosti promenljivih. Mislim da ću tek sutra moći da ti pošaljem polinom, ali samo da znaš da je mnogo "ružan".

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

Teoreticar
Galileo Galilej
Tuzla

Član broj: 129740
Poruke: 161
*.PPPoE-6518.sa.bih.net.ba.

+1 Profil

Re: Formula za "izbacivanje" svih prostih brojeva

^{12.11.2008. u 20:51 - pre 199 meseci}

Ok, hvala ti mnogo,kad stignes napisi nam...

Pa cekaj, kada se taj polinom odredio...koje godine?
Jer, zadnjih godina stalno se govori da ne postoji formula za dobijanje SVIH prostih brojeva.
Prosvetlite me?

Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.dynamic.sbb.rs.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+621 Profil

Re: Formula za "izbacivanje" svih prostih brojeva

^{12.11.2008. u 22:20 - pre 199 meseci}

Evo tog polinoma:

Moguće je poboljšati bilo stepen polinoma, bilo broj promenljivih. U prvom slučaju postoji polinom stepena

, ali on koristi

promenljive. Broj promenljivih je pak moguće svesti na

, no tada je stepen polinoma otprilike

.

_{[Ovu poruku je menjao Bojan Basic dana 13.11.2008. u 13:49 GMT+1]}

Ljubičice crvena, što si plava kô zelena trava.

Odgovor na temu

miki069

Član broj: 161528
Poruke: 2056
212.62.55.*

+390 Profil

Re: Formula za "izbacivanje" svih prostih brojeva

^{12.11.2008. u 23:51 - pre 199 meseci}

Ako ti nešta znači imam napisano programče u Delphi-ju koji za nekih 60 sekundi (na PIV računaru) izgeneriše prvih 4 000 000 prostih brojeva.

Statistika pojave je sledeća:

- 1 000 prost broj je 7 919 (svaki osmi u proseku je prost),
- 10 000 prost broj je 104 729 (svaki deseti u proseku),
- 100 000 prost broj je 1 299 709 (svaki trinaesti u proseku),
- 1000 000 prost broj je 15 485 709 (svaki petnaesti u proseku),
- 4 000 000 prost broj je 67 667 969 (svaki sedamnaesti u proseku),
- 10 000 000 prost broj je 179 424 691 (svaki osamnaesti u proseku).

I tako sve su redji i redji... Al ih ima beskonačno mnogo...
Vidi se da i tempo rasta koeficijenta razredjenosti polako pada...
Da li taj koeficijent ima maximum (gornji limes konačan) kome polako teži?
Ili i taj koeficijent teži beskonačnosti a njih opet ima beskonačno mnogo? Što je moguće ali je neinteresantno.
Ili on već postoji a ja ga ne znam?

Nemam programski odgovor jer ograničenje mi je LONGINT (mislim 2 na 64) u Delphi-ju. Ne mogu ga pustiti do beskonačnosti.
Vreme nije problem.Ovaj skor je sa pisanjem rezultata u txt fajl. Moram onda malo da ga preradim.

Ako ti nešta znači mogu ti dati to programče.

_{[Ovu poruku je menjao miki069 dana 13.11.2008. u 02:15 GMT+1]}

Odgovor na temu

Teoreticar
Galileo Galilej
Tuzla

Član broj: 129740
Poruke: 161
*.PPPoE-6518.sa.bih.net.ba.

+1 Profil

Re: Formula za "izbacivanje" svih prostih brojeva

^{13.11.2008. u 00:19 - pre 199 meseci}

Hvala miki ,ali ne treba za sada...
Hvala Bojane...
Ovo me malo zbunjuje ,jer polinom je faktorisan na dva izraza od kojih je jedan k+2 i ovaj u drugoj velikoj zagradi.Pa onda imamo UVEK proizvod dva cela broja ??

Odgovor na temu

987654321

Član broj: 196314
Poruke: 10
91.185.102.*

Profil

Re: Formula za "izbacivanje" svih prostih brojeva

^{13.11.2008. u 08:11 - pre 199 meseci}

A da mozda tu ne koristi Rimanova zeta funkcija...

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dynamic.sbb.rs.

+2801 Profil

Re: Formula za "izbacivanje" svih prostih brojeva

^{13.11.2008. u 11:04 - pre 199 meseci}

Umesto

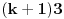
treba da stoji

.

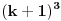
No, ako je polinom tacan i ovako faktorisan, to znaci da postoje dve vrednosti za

(0 i -2) za koje je vrednost polinoma pozitivna.

Postojanje ovakvog polinoma nije nikakva specificnost skupa prostih brojeva. Podkup skupa prirodnih brojeva se moze ovako predstaviti akko je rekurzivno nabrojiv. Primera radi, ovako se moze predstaviti skup svih prirodnih brojeva n, takvih da je zbir cifara broja n^n!-n! deljiv sa n²+7.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dynamic.sbb.rs.

+2801 Profil

Re: Formula za "izbacivanje" svih prostih brojeva

^{13.11.2008. u 11:06 - pre 199 meseci}

miki069

O raspodeli niza prostih brojeva govori teorema o prostim brojevima (prime number theorem).

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

Teoreticar
Galileo Galilej
Tuzla

Član broj: 129740
Poruke: 161
91.191.35.*

+1 Profil

Re: Formula za "izbacivanje" svih prostih brojeva

^{13.11.2008. u 11:12 - pre 199 meseci}

Ali za ako je k jednako -2 onda je vrijednost polinoma nula, jer je jedan faktor k+2

Odgovor na temu

uranium
Beograd

Član broj: 60097
Poruke: 543
79.101.200.*

Jabber: uranium@elitesecurity.org
ICQ: 324386953

+5 Profil

Re: Formula za "izbacivanje" svih prostih brojeva

^{13.11.2008. u 12:36 - pre 199 meseci}

Citat:

Teoreticar:
Ovo me malo zbunjuje ,jer polinom je faktorisan na dva izraza od kojih je jedan k+2 i ovaj u drugoj velikoj zagradi.Pa onda imamo UVEK proizvod dva cela broja ??

Citat:

Matijasevic's polynomial

Notice that this polynomial factors! Look at the special form of the second part: it is one minus a sum of squares, so the only way for it to be positive is for each of the squared terms to be zero (this is a trick of Putnam's).

... bilo je već sličnih tema:
http://www.elitesecurity.org/p810683

_{Attempt all the problems. Those you can do, don't do. Do the ones you cannot.}

Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.dynamic.sbb.rs.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+621 Profil

Re: Formula za "izbacivanje" svih prostih brojeva

^{13.11.2008. u 13:01 - pre 199 meseci}

Citat:

miki069:
Vidi se da i tempo rasta koeficijenta razredjenosti polako pada...
Da li taj koeficijent ima maximum (gornji limes konačan) kome polako teži?

Ne znam šta podrazumevaš pod „tempom rasta koeficijenta razređenosti“, ali ovo u zagradi (svaki ... u proseku) asimptotski je

(dokazano), pa vidi da li to odgovara na tvoje pitanje.

Ljubičice crvena, što si plava kô zelena trava.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dynamic.sbb.rs.

+2801 Profil

Re: Formula za "izbacivanje" svih prostih brojeva

^{13.11.2008. u 13:46 - pre 199 meseci}

Citat:

Teoreticar: Ali za ako je k jednako -2 onda je vrijednost polinoma nula, jer je jedan faktor k+2

OK,

. Jeli sada bolje?

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dynamic.sbb.rs.

+2801 Profil

Re: Formula za "izbacivanje" svih prostih brojeva

^{13.11.2008. u 13:49 - pre 199 meseci}

Citat:

uranium: Notice that this polynomial factors! Look at the special form of the second part: it is one minus a sum of squares, so the only way for it to be positive is for each of the squared terms to be zero (this is a trick of Putnam's).

Stvarno, ako je poenta u tome da svi kvadrati budu nule, sta onda radi faktor k+2?

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

Teoreticar
Galileo Galilej
Tuzla

Član broj: 129740
Poruke: 161
*.PPPoE-603.sa.bih.net.ba.

+1 Profil

Re: Formula za "izbacivanje" svih prostih brojeva

^{13.11.2008. u 14:17 - pre 199 meseci}

Da rezimiramo:
Skup pozitivnih vrednosti polinoma kojeg je napisao gosp. Bojan jednak je skupu prostih brojeva, polinom daje SVE proste brojeve za proizvoljne vrednosti promenljivih , gdje k može ima samo dve vrednosti i to:k=-1 v k=-3
Jeli sad sve OK?

Evo još neki polinomi prvog stepena, nista posebno...

Prikačeni fajlovi

O prostim brojevima.doc - 19.5k

Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.dynamic.sbb.rs.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+621 Profil

Re: Formula za "izbacivanje" svih prostih brojeva

^{13.11.2008. u 14:30 - pre 199 meseci}

Citat:

Nedeljko:
Stvarno, ako je poenta u tome da svi kvadrati budu nule, sta onda radi faktor k+2?

Faktor

je upravo prost broj koji dobiješ kao rezultat polinoma kada promenljivima dodeliš vrednosti. Dakle, prost broj

dobićeš za

(i pogodne vrednosti ostalih slova), dok nema načina da vrednost polinoma bude pozitivna za npr.

Citat:

Teoreticar:
...gdje k može ima samo dve vrednosti i to:k=-1 v k=-3
Jeli sad sve OK?

Ne (vidi prethodni pasus).

Ljubičice crvena, što si plava kô zelena trava.

Odgovor na temu