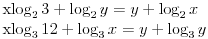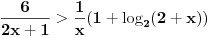2. Oblast definisanosti nejednačine je
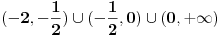
(zbog imenilaca i logaritma). Razmatraćemo dva slučaja:
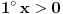
Za pozitivno

orijentacija nejednačine ne menja se pri množenju sa

, pa posle sređivanja i eliminisanja logaritma dobijamo
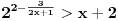
.
Za
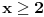
je
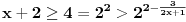
, pa tu rešenja nema i dovoljno je ispitati interval
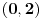
. Posmatrajmo funkciju
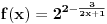
, definisanu za
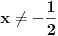
, i pravu
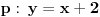
. Prvi izvod funkcije

je
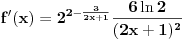
. Lako se proverava da je na datom intervalu drugi izvod svuda negativan. Dakle, funkcija je konkavna, što znači da je svaka tangenta tangira odozgo. Uzmimo tangentu u tački
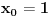
. Tu je
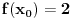
i
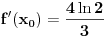
, pa jednačina tangente glasi
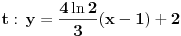
.
Iz
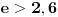
sledi
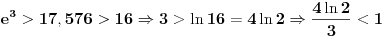
. Stoga
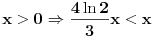
, pa je
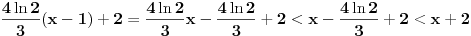
. Znači, prava

je uvek iznad prave

, a samim tim i iznad krive
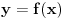
, te nejednačina u ovom slučaju nema rešenja.
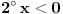
Zbog toga što u ovom slučaju množenje sa

menja orijentaciju nejednačine, ona će posle sređivanja glasiti
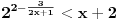
.
Ovde razmatramo dva podintervala:
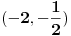
i
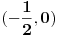
. Za interval
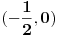
možemo opet iskoristiti krivu
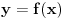
i prave

i

iz prethodnog slučaja, i lako pokazati da je prava

i na tom intervalu iznad krive
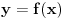
. Međutim, pošto je u odnosu na prethodni slučaj nejednačina obratno orijentisana, sledi da je ona na tom intervalu
zadovoljena. Što se tiče intervala
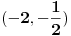
, tu imamo
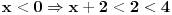
i
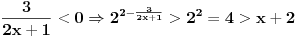
, pa nejednačina tu nema rešenja.
Zaključak: Skup rešenja date nejednačine je interval
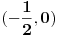 [Ovu poruku je menjao Farenhajt dana 30.12.2005. u 06:11 GMT+1]
[Ovu poruku je menjao Farenhajt dana 30.12.2005. u 06:11 GMT+1]