Ovo ce biti malo duza poruka. Ukratko, ono sto hocu da kazem je da ako imas:
- temperaturu gasa u zavisnosti od zapremine i pritiska
- unutrasnju energiju sistema u zavisnosti od zapremine i pritiska
- radni ciklus sistema definisan na p-V diagramu
onda mozes cisto matematicki da izracunas efikasnost sistema.
Ovo direktno daje odgovore na:
1. Koji je idealni ciklus bolji, Diesel ili Otto
2. Koji je idealni ciklus bolji, Brayton ili Atkinson
Uz malo razmisljanja onda mozes da odgovoris i na:
3. Zasto gubici pri kompresiji i ekspanziji brzo promijene redoslijed ciklusa u odgovoru na pitanja 1 i 2.
(ja nisam razmislio ali bi trebalo da bude lako)
Uz vise razmisljanja mozda ces moci da nadjes i odgovor na:
4. Na koji nacin je moguce povecati snagu Braytonovog ciklusa intervencijim na strani kompresora, a da pri tom najvisi pritisak u ciklusu i najvisa temperatura u ciklusu ostanu nepromijenjeni.
(nisam razmislio pa ne znam)
Sto se PBMR tice:
N i He razlikuju se po tome sto je N dvoatomski a He jednoatomski gas. To menja izraz za unutrasnju energiju od
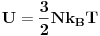
za He u
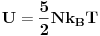
za N2
gde je
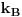
Botzmann-ova konstanta a N broj atoma/molekula.
U ova oba slucaja, vazi
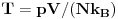
.
Sada detalji:
Zamisli da imas sud sa nekim gasom. Ako atoma gasa u sudu ima puno, ponasanja gasa moguce je opisati statistickom fizikom.
U okviru ovog statistickog opisa naci ce se i veza izmedju pritiska gasa (p), njegove zapremine (V) i temperature (T) u obliku
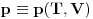
Unutrasnja energija gasa bice takodje funkcija temperature i zapremine:
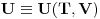
Prvu formulu moguce je cesto okrenuti i pisati
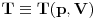
Zamenom u drugu formulu odmah dobijamo
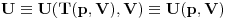
Note:
************************************************************************************************************
Ako cestice gasa medjusobno ne interaguju, vazice:
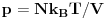
gde je
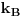
Boltzmann-ova konstanta a N broj cestica gasa (jednacina stanja idealnog gasa)
i takodje
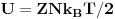
gde je Z prirodan broj koji odgovara broju unutrasnjih stanja svake cestice gasa.
U ovom slucaju:
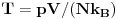
i
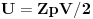
Ove rezultate mozes da nadjes u bilo kom udzbeniku *statisticke fizike* (*ne* termodinamike)
************************************************************************************************************
Zamisli sada da se sud sa gasom podvrgne nekom procesu koji menja p, V i T. Posto je T funkcija p i V (vidi gore), ovakav proces potpuno je zadat linijom na p-V dijagramu.
Posmatrajmo sad infinitezimalan p-V proces. Gas svojim pritiskom deluje na zidove suda. Stoga, ako se ti zidovi pomere, gas vrsi rad dA = p dV. Ako ovo nije jasno, zamisli cilindrican sud sa klipom na jednom kraju. Gas deluje na povrsinu A klipa silom F = A p. Ako se klip pomeri za rastojanje dx, rad gasa bice F dx odnosno A p dx = p dV.
U isto vreme, posto se p i V menjaju, menja se i unutrasnja energija gasa kao
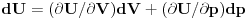
.
Energija za promenu unutrasnje energije gasa + rad koji gas vrsi mora da dodje odnekud. To "odnekud" je neki rezervar sa kojim je gas u kontaktu. Toplota koju rezervar predaje sistemu pri malom pomeraju na p-V dijagramu bice
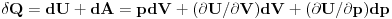
Pri tome, ako
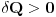
, sistem prima toplotu od rezervara dok ako
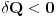
, sistem oslobadja toplotu u hladnjak.
Ovo je sve sto je potrebno za odredjivanje efikasnosti toplotne masine. Jer, toplotna masina krece iz stanja A, radi nesto i vraca se u stanje A, iscrtavajuci neku zatvorenu krivu C na p-V dijagramu. Ukupan rad koji masina pri tome odradi je
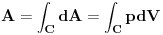
Da bi sracunali ulozenu toplotu, uzimamo samo delove ciklusa gde
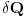
> 0:
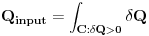
Efikasnost ciklusa/masine je onda
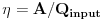
.
Za kraj, preporucujem ti da obavezno na netu nadjes i procitas barem o Karnoovom ciklusu (Carnot heat engine).
Pozdrav,
Marko